Engranatges: tot el que necessites saber sobre aquestes rodes dentades

Els engranatges estan en multitud de mecanismes actuals, des de rellotges analògics, fins a motors de vehicles, caixes de canvis, passant per robots, impressores, i molts altres sistemes mecatrònics. Gràcies a ells es poden realitzar sistemes de transmissió i anar més enllà de transmetre el moviment, també poden alterar-lo.

Per això, són elements molt importants que hauries de conèixer com funcionen de forma adequada. D'aquesta manera, podràs fer servir els engranatges adequats per als teus projectes i comprendre millor la forma en què operen ...

Què és un engranatge?

Existeixen els sistemes de cadenes, els de politges, les rodes de fricció, etc. tots ells sistemes de transmissió amb els seus avantatges i desavantatges. Però de tots ells destaca el sistema d'engranatges, que solen ser els favorits per les seves propietats:

• Poden resistir grans forces causa de les seves dents sense que llisquin, com li podria passar a les rodes de fricció o politges.
• És un sistema reversible, capaç de transmetre potència o moviment en tots dos sentits.
• Permeten un control de moviment molt precís, com es pot comprovar en els motors pas a pas, Per exemple.
• Permeten crear sistemes de transmissió compactes enfront de les cadenes o politges.
• Es poden combinar diferents mides per interferir en el gir de cada eix. En general, quan es fan servir dues rodes dentades, a l'engranatge més gran se l'anomena roda i a el petit pinyó.

Un engranatge o roda dentada no és més que un tipus de roda amb una sèrie de dents tallats en la seva vora extern o intern, depenent de el tipus d'engranatge que sigui. Aquestes rodes dentades estaran en moviment rotatori per generar una torsió en els eixos als quals estan unides, i es poden agrupar per generar sistemes d'engranatges més complexos, encaixant les seves dents.

Evidentment, perquè això sigui possible, el tipus i mida de les dents ha de coincidir. Altrament seran incompatibles i no encaixarien. Aquests paràmetres són els que es tracten en el proper apartat ...

Parts d'un engranatge

Perquè dos engranatges encaix entre si, es podria variar el diàmetre i quantitat de dents, però han de respectar una sèrie de factors que són els que fan que l'engranatge sigui compatible entre si, Com el tipus de dent que fan servir, les dimensions, etc.

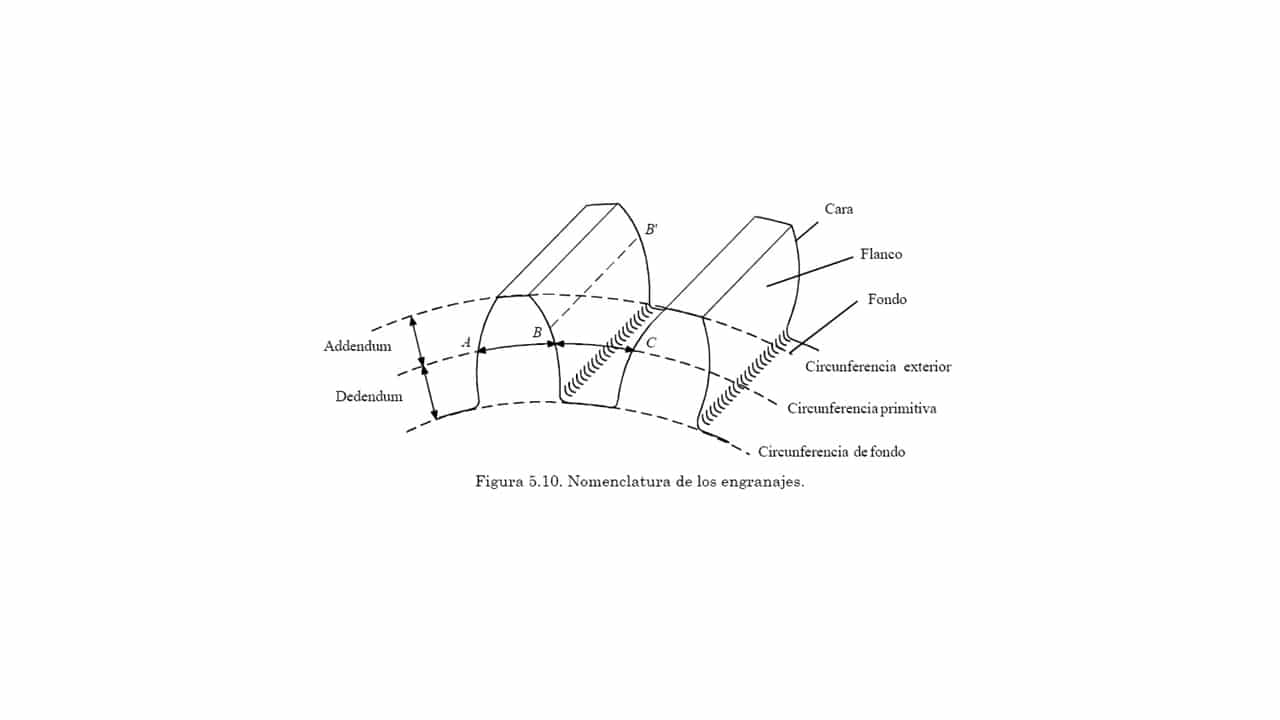
Com pots veure en la imatge anterior, hi ha diverses parts en un engranatge que hauries de conèixer:

• Envà o braços: És la part que s'encarrega d'unir la corona i el cub per poder transmetre el moviment. Poden ser més o menys gruixuts, i d'això i la seva composició dependrà en gran mesura la resistència i pes. De vegades se solen foradar parell reduir el pes, altres s'opta per un envà sòlid.
• cub: És la part on s'acobla l'eix de transmissió de moviment i que va unit a l'envà.
• Corona: És la zona de l'engranatge on s'han tallat les dents. És la més important, ja que d'ella dependrà la compatibilitat, comportament i prestacions de l'engranatge.
• dent: És una de les dents o protuberàncies de la corona. La dent pot subdividir en diverses parts:
  • cresta: És la part exterior o punta de la dent.
  • Cara i flanc: És la part superior i inferior de lateral de la dent, és a dir, la superfície de contacte entre dues rodes dentades que engranen.
  • vall: És la part inferior de la dent o zona intermèdia entre dues dents, on anirà allotjada la cresta d'una altra roda dentada amb la qual engrani.

Tot això genera una sèrie de geometries de corona que distingiran els tipus i propietats dels engranatges:

• circumferència arrel: Marca la vall o fons de les dents. És a dir, delimita el diàmetre interior de l'engranatge.
• circumferència primitiva: Estableix la divisió entre les dues parts de l'lateral de la dent: cara i flanc. És un paràmetre molt important, ja que en funció d'ella es defineixen totes les altres. Dividirà la dent en dues parts, el dedendum i l'addendum.
  • Peu de la dent o dedendum: És la part inferior de la dent que queda entre la circumferència primitiva i la circumferència arrel.
  • Cap de la dent o addendum: Zona superior de la dent, que va des de la circumferència primitiva i l'exterior.
• Circumferència de cap: Marcarà la cresta de les dents, és a dir, el diàmetre exterior de l'engranatge.

Com pots imaginar, en funció de la corona, diàmetre i tipus de dents, es pot variar l'engranatge segons:

• Nombre de dents: Definirà la relació de l'engranatge i és un dels paràmetres més determinants per determinar el seu comportament en un sistema de transmissió.
• Alçada de la dent: L'altura total, des de la vall fins a la carena.
• pas circular: Distància entre una part de la dent i la mateixa part del següent dent. És a dir, com de separats estan les dents, el que està també relacionat amb el nombre.
• espessor: És el gruix que té l'engranatge.

Aplicacions dels engranatges

Els aplicacions dels engranatges són moltes, com ja he comentat anteriorment. Algunes de les seves aplicacions pràctiques són:

• Caixes de canvis de vehicles.
• Motors pas a pas per al control de el gir.
• Bombes hidràuliques.
• Motors de tota mena, com a elements de transmissió de gir o moviment.
• Mecanismes diferencial.
• Impressores per moure els capçals o rodets.
• Robots per a les parts mòbils.
• Maquinària industrial.
• Rellotges analògics.
• Electrodomèstics amb parts mecàniques.
• Dispositius electrònics amb parts mòbils.
• Motors d'obertura de portes.
• Joguines mòbils.
• Maquinària agrícola.
• Aeronàutica.
• Producció d'energia (eòlica, tèrmica, ...).
• etcètera...

Tu pots pensar multitud d'aplicacions més per als teus projectes amb Arduino, robots, etc. Podràs automatitzar molts mecanismes i jugar amb les velocitats, etc.

Tipus d'engranatges

Segons les seves dents i de les característiques de l'propi engranatge tens diferents tipus d'engranatges al teu abast, cadascun amb els seus avantatges i desavantatges, de manera que és important triar l'adequat per a cada aplicació.

Els tipus més habituals són:

• cilíndrics: S'usen per eix paral·lels.
  • rectes: Són els més habituals, usats quan es necessita un engranatge simple amb velocitats no molt elevades.
  • helicoïdal: Són una versió una mica més avançada dels anteriors. En ells les dents estan disposats a trajectòries d'hèlixs paral·leles al voltant d'un cilindre (simples o dobles). Tenen un clar avantatge enfront dels rectes, com ser més silenciosos, operar a més altes velocitats, poden transmetre més potència, tenen un moviment més uniforme i segur.
• cònics: S'usen per a transmetre moviment entre eixos col·locats a diferents angles, fins i tot a 90º.
  • rectes: Fan servir dents rectes i comparteixen característiques amb els cilíndrics rectes.
  • en espiral: En aquest cas suporten majors velocitats i forces, com li passava als helicoïdals.
• engranatge intern: En comptes de tenir les dents o corona tallada per fora la tenen en la seva cara interna. No són tan habituals, però també s'utilitzen per a certes aplicacions.
• planetaris: És un conjunt d'engranatges emprat en certs sistemes de transmissió on hi ha un engranatge central al voltant de el qual giren altres més petits. Per això té aquest nom, ja que semblen estar orbitant.
• Cargol sense fi: És un engranatge habitual en alguns mecanismes industrials o electrònics. Empra un engranatge les dents estan tallats en forma d'espiral. Generen una velocitat molt constant i sense vibracions ni soroll. Poden transmetre a una roda dentada recta l'eix es trobi en oblic a el cargol sense fi.
• Cremallera i pinyó: És un conjunt d'engranatges també habitual en alguns mecanismes i que permet transformar un moviment rotatori d'un eix en un moviment lineal o viceversa.

Si s'atén a seva composició, També es pot diferenciar entre materials com:

• metalls: Solen ser de diferents tipus d'acer, aliatges de coure, aliatges d'alumini, ferro fos o fosa grisa, aliatges de magnesi, etc.
• Plàstics: S'empren en electrònica, joguines, etc. Són engranatges de policarbonat, poliamida o PVC, resines acetálicas, polieteretercetona PEEK, politetrafluoroetilè (PTFE), i polímers de cristall líquid (LCP).
• Fusta: No són habituals, només en mecanismes antics o en certs joguines.
• Altres: És probable que per a casos molt concrets s'utilitzin altres fibres o materials concrets.

On comprar engranatges?

Pots trobar diferents tipus d'engranatges en multitud de botigues de mecànica o electrònica. Per exemple, aquí tens alguns exemples:

• Kit d'engranatges de motor de plàstic. Amb 64 ​​tipus diferents.
• No s'ha trobat cap producte.
• Kit de 16 peces de metall diferents, inclosos helicoïdals.
• Kit d'engranatges de cargol de plàstic.

Aquests productes són de mida petita, si necessites engranatges més grans és probable que no els trobis tan fàcilment. A més, si necessites alguna cosa molt específic, molts tallers de torners poden fabricar-per a tu. Les impressores 3D també estan contribuint al fet que els makers puguin crear els seus propis engranatges.

Càlculs bàsics per als sistemes de rodes dentades

Com pots veure en aquest GIF, cal comprendre que quan dos engranatges s'engranen, tots dos eixos giraran en sentit contrari i no en el mateix sentit. Com veus, si observes la ruda dentada vermella està girant cap a la dreta, mentre la blava està fent-ho a l'esquerra.

Per tant, perquè un eix giri en la mateixa direcció caldria afegir una altra roda addicional, com la verda. D'aquesta manera, vermell i verd giren en la mateixa direcció. Això és degut al fet que, com blau girava cap a l'esquerra, a l'engranar blau-verd, verd tornarà a invertir el sentit de gir, sincronitza amb vermell.

Una altra de les coses que s'aprecien en aquest GIF és la velocitat de gir. Si tots els engranatges tinguessin el mateix diàmetre i nombre de dents, tots els eixos estarien rotant a igual velocitat. En canvi, quan s'altera el nombre de dent / diàmetre, també s'altera la velocitat. Com pots veure en aquest cas, vermell és la que gira més ràpid, a l'tenir menor diàmetre, mentre que blau gira a una velocitat mitjana i verd és la que més lent gira.

Atenent a això, es pot pensar que jugant amb les mides es poden alterar les velocitats. Estàs a la veritat, com una bicicleta pot fer-ho amb els canvis de marxes o la caixa de canvis ho fa amb les relacions de marxes d'un cotxe. I no només això, també es poden fer càlculs sobre la velocitat de gir.

Quan tens dos engranatges engranats, un petit (pinyó) i un altre gran (roda), Podria ocórrer el següent:

• Si imaginem que el motor o tracció s'aplica a el pinyó i la roda és arrossegada, encara que el pinyó giri a alta velocitat, a l'tenir una roda més gran, aquesta ho farà més lent, actuant com un reductor. Només si són de la mateixa mida (pinyó = roda) girarien els dos eixos en la mateixa velocitat.
• En canvi, si imaginem que és la roda la que té la tracció i se li aplica una velocitat, encara que sigui baixa, el pinyó estarà girant més ràpid, ja que la seva reduïda grandària actua com multiplicador.

Càlculs de transmissió entre engranatges

Un cop has assolit aquest concepte, es poden realitzar els càlculs d'un sistema de transmissió simple entre dos engranatges aplicant la fórmula:

N1 · Z1 = N2 · Z2

Sent Z el nombre de dents dels engranatges 1 i 2 que hi ha engranats i N és la velocitat de gir dels eixos en RPM (revolucions per minut o voltes per minut). per EXEMPLE, Imagina que al GIF anterior, per simplificar:

• Vermell (tracció) = 4 grans i el motor està aplicant una velocitat de gir al seu eix de 7 RPM.
• Blau = 8 dents
• Verd = 16 dents

Si es volgués calcular el gir en aquest sistema, primer s'ha de calcular la velocitat de el blau:

4 · 7 = 8 · z

z = 4 · 7/8

z = 3.5 RPM

És a dir, l'eix blau estaria girant a 3.5 RPM, una mica més lenta que les 4 RPM de l'vermell. Si volguessis calcular el gir de verd, ara que ja coneixes la velocitat de blau:

8 · 3.5 = 16 · z

z = 8 · 3.5/16

z = 1.75

Com pots veure, verd giraria a 1.75 RPM, la qual cosa és més lent que blau i verd. I què passaria si el motor està situat en l'eix de verd i és la roda tractora girant a 4 RPM, ja que llavors el gir seria de 8 RPM per blau, 16 RPM per a vermell.

Es dedueix així que, quan la roda de tracció és petita, a l'eix final s'aconsegueix una velocitat menor, però més força. En el cas que sigui la roda gran la que porta la tracció, s'aconsegueix a la petita una major velocitat, però menys força. Per què hi ha potències o parell de gir diferents? Observa aquesta fórmula:

P = T · ω

Sent P la potència transmesa per l'eix en watts (W), T el parell de forces desenvolupat (N · m), ω la velocitat angular a la que gira l'eix (rad / s). Si es manté la potència de el motor i es multiplica o redueix la velocitat de gir, llavors s'altera també T. El mateix passa si es manté T constant i es varia la velocitat, llavors P s'altera.

És probable que també vulguis calcular si un eix gira a X RPM, quant avançaria linealment, és a dir, la velocitat lineal. Per exemple, imagina que en el vermell tens un motor DC i en l'eix verd has col·locat una roda perquè un motor es desplaci per una superfície. A quina velocitat aniria avançaria?

Per a això, només has de calcular la circumferència de l'pneumàtic que has instal·lat. Per a això, multiplica el diàmetre per Pi i et donarà la circumferència. Coneixent el que pot avançar amb cada gir la roda i tenint en compte el que gira cada minut, es pot obtenir la velocitat lineal ...

Aquí et mostro un vídeo perquè puguis entendre això d'una millor manera:

Càlculs per cargol sense fi i roda dentada

Quant al cargol sense fi i la roda dentada, Es pot calcular amb la fórmula:

i = 1 / Z

Això és així perquè el cargol es considera en aquest sistema com una roda dentada d'una sola dent que ha estat tallada de forma helicoïdal. Per això, si tens una roda dentada de 60 dents, per exemple, llavors serà 1/60 (això vol dir que el cargol hauria de girar 60 vegades perquè la roda dentada completi 1 sol gir). A més, és un mecanisme que no és reversible com altres, és a dir, la roda dentada no es pot girar perquè giri el cargol sense fi, només el cargol sens fi pot ser l'eix tractor aquí.

Càlculs per pinyó i cremallera

Per al sistema de pinyó i cremallera, els càlculs tornen a variar, en aquest cas són:

V = (p · Z · N) / 60

És a dir, multiplicar el pas de les dents de l'pinyó (en metres), pel nombre de dents de l'pinyó, i pel nombre de girs de l'pinyó (en RPM). I això es divideix entre 60. Per exemple, imagina que tens un sistema amb un pinyó de 30 dents, un pas de 0.025 m, i una velocitat de gir de 40 RPM:

V = (0.025 · 30 · 40) / 60

V = 0.5 m / s

És a dir, avançaria mig metre cada segon. I, en aquest cas, sí que és reversible, És a dir, si es mou longitudinalment la cremallera es pot fer que giri el pinyó.

Fins i tot podries calcular quant trigaria a recórrer una distància tenint en compte la fórmula de moviment rectilini uniforme (V = d / t), és a dir, que si la velocitat és igual a la distància partit pel temps, llavors es buida el temps:

t = d / v

Per tant, coneixent ja la velocitat i la distància que vols calcular, per exemple, imagina que vols calcular quant trigaria a recórrer 1 metre:

t = 1 / 0.5

t = 2 segons

Espero haver-te ajudat a obtenir al menys els coneixements més essencials sobre els engranatges, perquè comprenguis com funcionen i com els pots utilitzar al teu favor en els teus futurs projectes.