Όπως το Ο νόμος του Ωμ, Η Οι νόμοι του Kirchhoff Είναι ένας από τους βασικούς κανόνες για την ηλεκτρονική. Αυτοί οι νόμοι μας επιτρέπουν να αναλύουμε την τάση και την ένταση ρεύματος σε έναν κόμβο, κάτι απαραίτητο για να γνωρίζουμε πτυχές των κυκλωμάτων.
Αν θέλετε μάθετε περισσότερα για αυτούςΣας καλώ να συνεχίσετε να διαβάζετε ολόκληρο το σεμινάριο για τις θεμελιώδεις εξισώσεις και την εφαρμογή τους σε βασικά κυκλώματα ...
Κόμβος, κλάδος, πλέγμα
Όταν αναλύετε ένα κύκλωμα, μπορείτε να διακρίνετε μεταξύ των διαφορετικών συμβόλων των στοιχείων, των γραμμών σύνδεσης, των συνδέσεων και επίσης τους κόμβους. Τα τελευταία ονομάζονται επίσης κλαδί ή πλέγμα.
Οι νόμοι του Kirchhoff χρησιμεύουν στην ανάλυση του ηλεκτρικές ιδιότητες σε αυτούς τους κόμβους. Δηλαδή, στα σημεία διασταύρωσης όπου δύο ή περισσότερα στοιχεία είναι αλληλένδετα. Για παράδειγμα, ως σημείο που μπορείτε να δείτε στην κύρια εικόνα αυτού του άρθρου ...
Οι νόμοι του Kirchhoff
ο Οι νόμοι του Kirchhoff Είναι δύο ισοτιμίες ή εξισώσεις που βασίζονται στις αρχές της εξοικονόμησης ενέργειας και της φόρτισης των ηλεκτρικών κυκλωμάτων. Και οι δύο νόμοι μπορούν να ληφθούν απευθείας με την εξαγωγή των διάσημων εξισώσεων Maxwell, αν και ο Kirchhoff το προηγήθηκε αυτό.
Το όνομά τους προέρχεται από τον ερευνητή τους, καθώς περιγράφηκαν για πρώτη φορά το 1846 από τον Gustav Kirchhoff. Και σήμερα χρησιμοποιούνται ευρέως στη μηχανική ηλεκτρικές και ηλεκτρονικές για να γνωρίζουν την τάση και το ρεύμα στους κόμβους κυκλώματος, και μαζί με τον Νόμο του Ohm, αποτελούν πολύ αποτελεσματικά εργαλεία για ανάλυση.
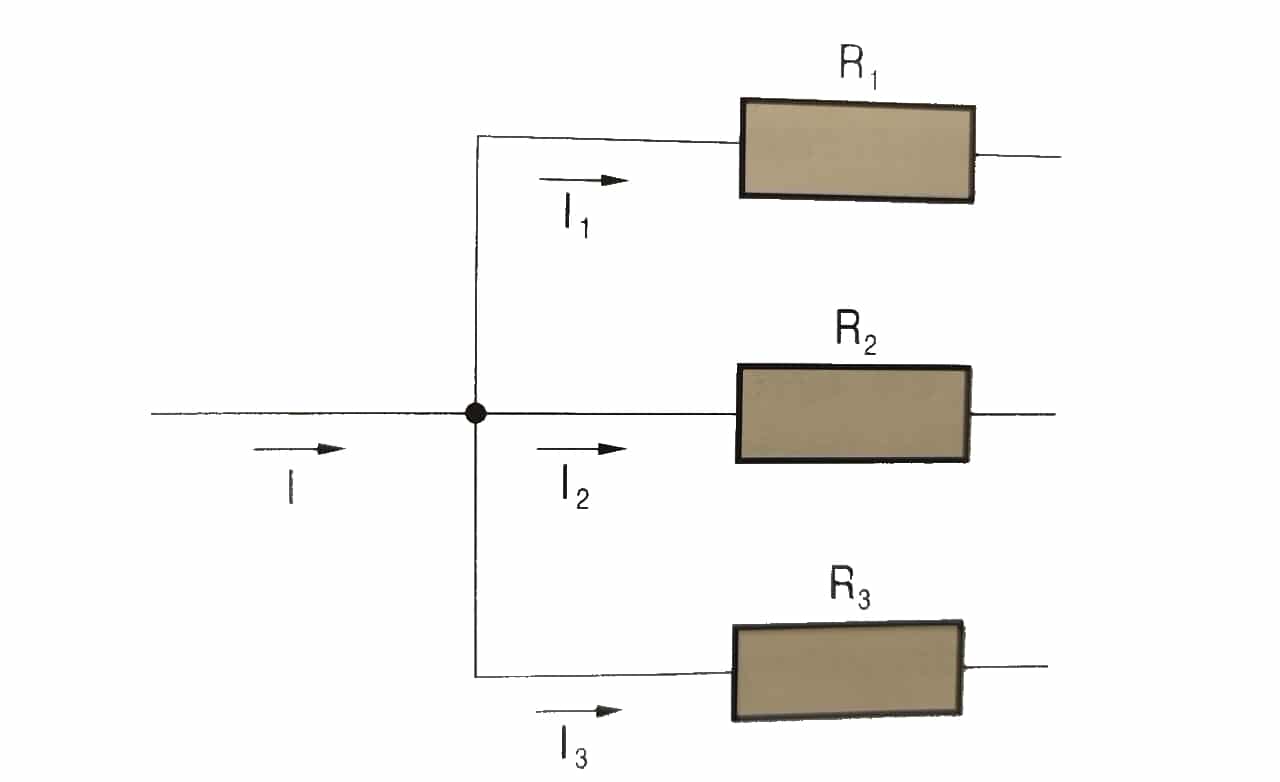
Πρώτος νόμος ή κόμβοι
«Σε οποιονδήποτε κόμβο, το αλγεβρικό άθροισμα των εντάσεων που εισέρχονται σε έναν κόμβο είναι ίσο με το αλγεβρικό άθροισμα των εντάσεων που το αφήνουν. Ομοίως, το άθροισμα όλων των ρευμάτων μέσω του κόμβου είναι μηδέν.»
I = εγώ1 + Ι2 + Ι3…
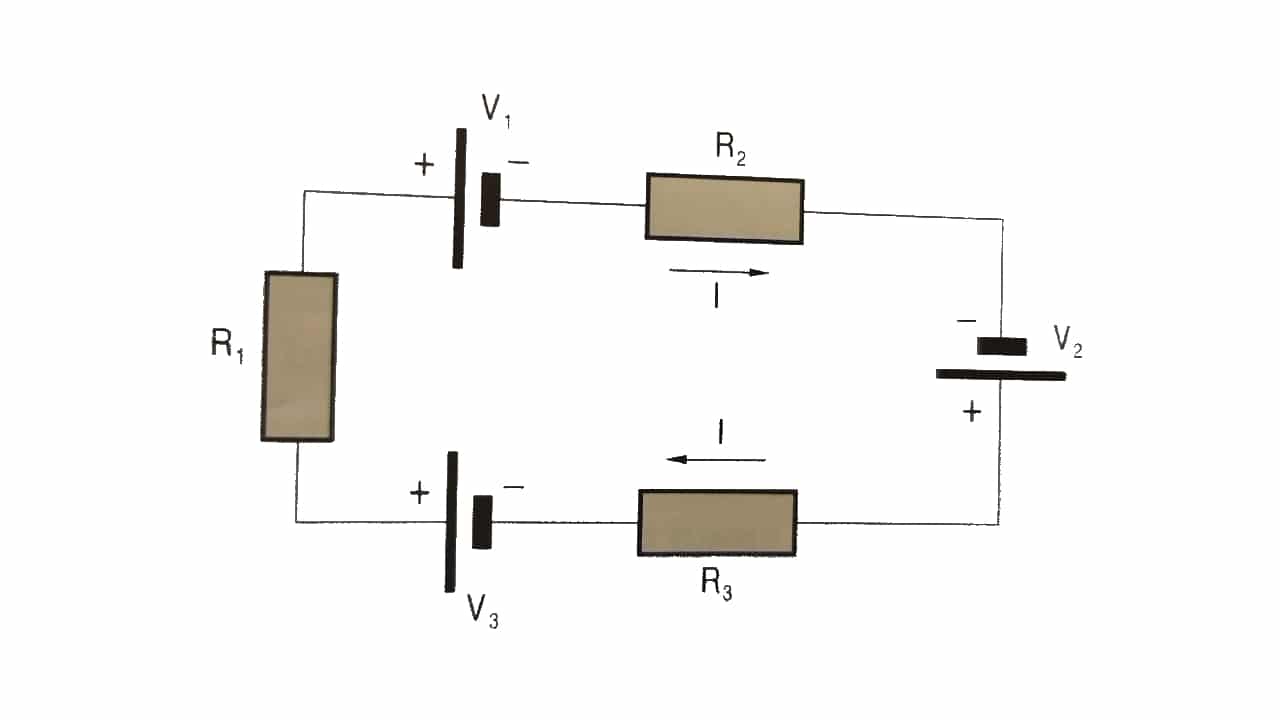
Δεύτερος νόμος ή πλέγματα
«Σε κλειστό κύκλωμα, το άθροισμα όλων των πτώσεων τάσης ισούται με τη συνολική παρεχόμενη τάση. Ομοίως, το αλγεβρικό άθροισμα των διαφορών ηλεκτρικού δυναμικού σε ένα κύκλωμα ισούται με μηδέν.".
-V1 + V2 + V3 = I R1 + Εγώ2 + Εγώ3 = Ι (R1 + R2 + R3)
Τώρα μπορείτε να αρχίσετε να τα εφαρμόζετε απλοί τύποι για να λάβετε τις λεπτομέρειες του ρεύματος και της τάσης στα κυκλώματά σας ...