Gears: όλα όσα πρέπει να γνωρίζετε για αυτά τα γρανάζια

Ο γρανάζια Βρίσκονται σε πληθώρα τρεχόντων μηχανισμών, από αναλογικά ρολόγια, έως κινητήρες οχημάτων, κιβώτια ταχυτήτων, μέσω ρομπότ, εκτυπωτών και πολλών άλλων μηχατρονικών συστημάτων. Χάρη σε αυτά, μπορούν να δημιουργηθούν συστήματα μετάδοσης και να ξεπερνούν την κίνηση μετάδοσης, μπορούν επίσης να το αλλάξουν.

Επομένως, είναι πολύ σημαντικά στοιχεία που πρέπει να ξέρετε πώς λειτουργούν Σωστά. Με αυτόν τον τρόπο, μπορείτε να χρησιμοποιήσετε τα σωστά εργαλεία για τα έργα σας και να κατανοήσετε καλύτερα πώς λειτουργούν ...

Τι είναι το γρανάζι;

Υπάρχουν συστήματα αλυσίδας, συστήματα τροχαλίας, τροχοί τριβής κ.λπ. Ολα τους συστήματα μετάδοσης με τα πλεονεκτήματα και τα μειονεκτήματά του. Αλλά από όλα αυτά, το σύστημα ταχυτήτων ξεχωρίζει, τα οποία είναι συνήθως αγαπημένα για τις ιδιότητές τους:

• Μπορούν να αντέξουν μεγάλες δυνάμεις λόγω των δοντιών τους χωρίς ολίσθηση, όπως θα μπορούσε να συμβεί σε τροχούς τριβής ή τροχαλίες.
• Είναι ένα αναστρέψιμο σύστημα, ικανό να μεταδίδει ισχύ ή κίνηση και προς τις δύο κατευθύνσεις.
• Επιτρέπουν πολύ ακριβή έλεγχο κίνησης, όπως φαίνεται στο κινητήρες stepper, Για παράδειγμα.
• Επιτρέπουν τη δημιουργία συμπαγών συστημάτων μετάδοσης μπροστά από τις αλυσίδες ή τις τροχαλίες.
• Διαφορετικά μεγέθη μπορούν να συνδυαστούν για να επηρεάσουν την περιστροφή κάθε άξονα. Γενικά, όταν χρησιμοποιούνται δύο γρανάζια, το μεγαλύτερο γρανάζι ονομάζεται τροχός και το μικρό γρανάζι.

Un γρανάζι ή γρανάζια δεν είναι τίποτα περισσότερο από έναν τύπο τροχού με μια σειρά από δόντια σκαλισμένα στο εξωτερικό ή το εσωτερικό του άκρο, ανάλογα με τον τύπο του γραναζιού. Αυτά τα γρανάζια θα είναι σε περιστροφική κίνηση για να παράγουν ροπή στους άξονες στους οποίους είναι προσαρτημένα και μπορούν να ομαδοποιηθούν για να δημιουργήσουν πιο πολύπλοκα συστήματα μετάδοσης, προσαρμόζοντας τα δόντια τους.

Προφανώς, για να είναι εφικτό, τον τύπο και το μέγεθος των δοντιών πρέπει να ταιριάζουν. Διαφορετικά θα είναι ασυμβίβαστες και δεν θα ταιριάζουν. Αυτές οι παράμετροι συζητούνται στην επόμενη ενότητα ...

Μέρη γραναζιού

Για να ταιριάζουν δύο γρανάζια, η διάμετρος και ο αριθμός των δοντιών θα μπορούσαν να ποικίλουν, αλλά πρέπει να σέβονται μια σειρά παραγόντων που είναι αυτό που κάνει το γρανάζι να είναι συμβατά μεταξύ τους, όπως ο τύπος των δοντιών που χρησιμοποιούν, οι διαστάσεις κ.λπ.

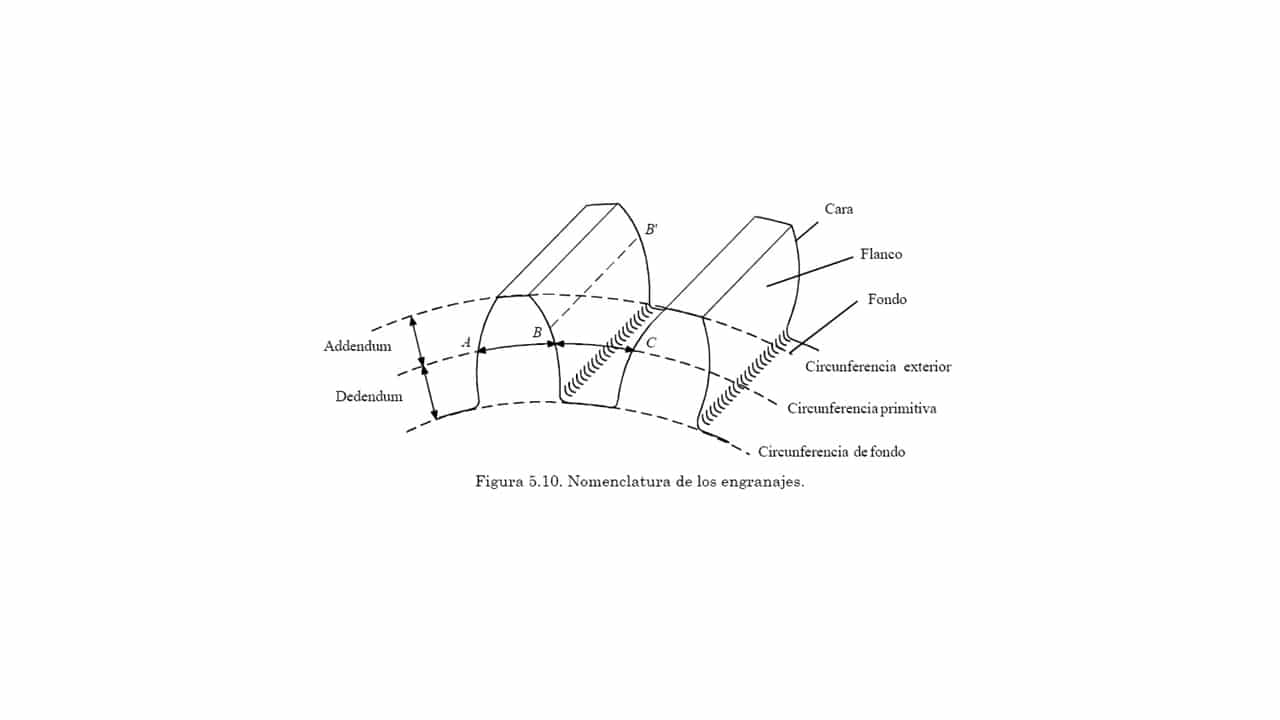
Όπως μπορείτε να δείτε στην προηγούμενη εικόνα, υπάρχουν διάφορα μέρη σε μια ταχύτητα πρέπει να γνωρίζετε:

• Σήπιο ή όπλα: είναι το μέρος που είναι υπεύθυνο για την ένωση της κορώνας και του κύβου για τη μετάδοση της κίνησης. Μπορούν να είναι λίγο πολύ παχιά, και η σύνθεση και η αντοχή του εξαρτώνται σε μεγάλο βαθμό από τη δύναμη και το βάρος. Μερικές φορές συνήθως διαπερνούνται για να μειώσουν το βάρος, άλλες φορές επιλέγεται ένα στερεό διαμέρισμα.
• Κύβος: είναι το μέρος όπου είναι συνδεδεμένος ο άξονας μετάδοσης κίνησης και είναι συνδεδεμένος στο διαμέρισμα.
• Corona: είναι η περιοχή του γραναζιού όπου έχουν κοπεί τα δόντια. Είναι το πιο σημαντικό, καθώς η συμβατότητα, η συμπεριφορά και η απόδοση του γραναζιού θα εξαρτηθεί από αυτήν.
• Δόντι: είναι ένα από τα δόντια ή τις προεξοχές της κορώνας. Το δόντι μπορεί να υποδιαιρεθεί σε διάφορα μέρη:
  • Κρέστα: είναι το εξωτερικό μέρος ή το άκρο του δοντιού.
  • Πρόσωπο και πλευρά: είναι το άνω και κάτω μέρος της πλευράς του δοντιού, δηλαδή η επιφάνεια επαφής μεταξύ δύο γραναζιών που πλέουν.
  • Valle: είναι το κάτω μέρος του δοντιού ή η ενδιάμεση περιοχή ανάμεσα σε δύο δόντια, όπου η κορυφή ενός άλλου οδοντωτού τροχού με τον οποίο θα στερεώνεται.

Όλα αυτά δημιουργούν μια σειρά από γεωμετρίες κορώνας που θα διακρίνει τους τύπους και τις ιδιότητες των γραναζιών:

• Περιφέρεια ρίζας: σηματοδοτεί την κοιλάδα ή το κάτω μέρος των δοντιών. Δηλαδή, οριοθετεί την εσωτερική διάμετρο του γραναζιού.
• Πρωτόγονη περιφέρεια: καθιερώνει τη διαίρεση μεταξύ των δύο τμημάτων της πλευράς του δοντιού: πρόσωπο και πλευρά. Είναι μια πολύ σημαντική παράμετρος, καθώς όλες οι άλλες ορίζονται βάσει αυτής. Θα χωρίσει το δόντι σε δύο μέρη, το δένδρο και το προσθήκη.
  • Δόντι ή πόδι: είναι η κάτω περιοχή του δοντιού που βρίσκεται μεταξύ της αρχικής περιφέρειας και της περιφέρειας της ρίζας.
  • Κεφάλι δοντιού ή προσθήκη: άνω περιοχή του δοντιού, η οποία πηγαίνει από την αρχική περιφέρεια και την εξωτερική περιφέρεια.
• Περίμετρος κεφαλιού- θα σηματοδοτήσει την κορυφή του δοντιού, δηλαδή την εξωτερική διάμετρο του γραναζιού.

Όπως μπορείτε να φανταστείτε, ανάλογα με την κορώνα, τη διάμετρο και τους τύπους των δοντιών, μπορείτε ποικίλλουν γρανάζια σύμφωνα με:

• Αριθμός δοντιών: θα καθορίσει την αναλογία γραναζιού και είναι μια από τις πιο καθοριστικές παραμέτρους για τον προσδιορισμό της συμπεριφοράς της σε ένα σύστημα μετάδοσης.
• Ύψος δοντιών: το συνολικό ύψος, από την κοιλάδα έως την κορυφογραμμή.
• Κυκλικό βήμα: απόσταση μεταξύ ενός μέρους του δοντιού και του ίδιου μέρους του επόμενου δοντιού. Δηλαδή, πόσο μακριά είναι τα δόντια, που σχετίζεται επίσης με τον αριθμό.
• Πάχος: είναι το πάχος του γραναζιού.

Εφαρμογές εργαλείων

ο εφαρμογές γραναζιών υπάρχουν πολλά, όπως έχω ήδη σχολιάσει προηγουμένως. Μερικές από τις πρακτικές εφαρμογές του είναι:

• Κιβώτια ταχυτήτων οχήματος.
• Βηματικοί κινητήρες για έλεγχο περιστροφής.
• Υδραυλικές βόμβες.
• Κινητήρες όλων των ειδών, όπως στοιχεία στροφής ή μετάδοσης κίνησης.
• Διαφορετικοί μηχανισμοί.
• Εκτυπωτές για μετακίνηση κεφαλών ή κυλίνδρων.
• Ρομπότ για κινούμενα μέρη.
• Βιομηχανικά μηχανήματα.
• Αναλογικά ρολόγια.
• Οικιακές συσκευές με μηχανικά μέρη.
• Ηλεκτρονικές συσκευές με κινούμενα μέρη.
• Κινητήρες ανοίγματος πόρτας.
• Κινητά παιχνίδια.
• Γεωργικά μηχανήματα.
• Αεροναυτική.
• Παραγωγή ενέργειας (αιολική, θερμική, ...).
• και ούτω καθεξής

Μπορείτε να σκεφτείτε πολλές άλλες εφαρμογές για τα έργα σας με Arduino, ρομπότ κ.λπ. Μπορείτε να αυτοματοποιήσετε πολλούς μηχανισμούς και να παίξετε με ταχύτητες κ.λπ.

Τύποι εργαλείων

Σύμφωνα με τα δόντια του και τα χαρακτηριστικά του ίδιου του εργαλείου, έχετε διαφορετικοί τύποι γραναζιών στα χέρια σας, το καθένα με τα πλεονεκτήματα και τα μειονεκτήματά του, οπότε είναι σημαντικό να επιλέξετε το σωστό για κάθε εφαρμογή.

Ο πιο συνηθισμένους τύπους ήχου:

• Κυλινδρικός: χρησιμοποιούνται για παράλληλους άξονες.
  • Ευθεία: είναι τα πιο συνηθισμένα, χρησιμοποιούνται όταν απαιτείται απλή ταχύτητα με πολύ υψηλές ταχύτητες.
  • Ελικοειδής: είναι μια κάπως πιο προηγμένη έκδοση των προηγούμενων. Σε αυτά τα δόντια είναι διατεταγμένα σε παράλληλες ελικοειδείς διαδρομές γύρω από έναν κύλινδρο (μονό ή διπλό). Έχουν ένα σαφές πλεονέκτημα έναντι των ευθειών, όπως είναι πιο αθόρυβο, λειτουργούν σε υψηλότερες ταχύτητες, μπορούν να μεταδίδουν περισσότερη ισχύ και να έχουν πιο ομοιόμορφη και ασφαλή κίνηση.
• Κωνικός: χρησιμοποιούνται για τη μετάδοση κίνησης μεταξύ αξόνων τοποθετημένων σε διαφορετικές γωνίες, ακόμη και σε 90º.
  • Ευθεία: χρησιμοποιούν ίσια δόντια και μοιράζονται χαρακτηριστικά με τα ευθύγραμμα κυλινδρικά.
  • Σπειροειδής: σε αυτήν την περίπτωση υποστηρίζουν υψηλότερες ταχύτητες και δυνάμεις, όπως συνέβη με τις ελικοειδείς.
• Εσωτερικό γρανάζι: αντί να έχουν λαξευτεί τα δόντια ή το στέμμα στο εξωτερικό, το έχουν στο εσωτερικό. Δεν είναι τόσο κοινές, αλλά χρησιμοποιούνται επίσης για ορισμένες εφαρμογές.
• Πλανητάρια: είναι ένα σετ γραναζιών που χρησιμοποιείται σε ορισμένα συστήματα μετάδοσης όπου υπάρχει ένα κεντρικό γρανάζι γύρω από το οποίο περιστρέφονται άλλα μικρότερα. Αυτός είναι ο λόγος για τον οποίο έχει αυτό το όνομα, καθώς φαίνεται να είναι σε τροχιά.
• Ατελείωτη βίδα: είναι ένα κοινό εργαλείο σε ορισμένους βιομηχανικούς ή ηλεκτρονικούς μηχανισμούς. Χρησιμοποιεί γρανάζι του οποίου τα δόντια κόβονται σε σπειροειδές σχήμα. Παράγουν μια πολύ σταθερή ταχύτητα και χωρίς δονήσεις ή θόρυβο. Μπορούν να μεταδώσουν σε έναν ευθύ τροχό, του οποίου ο άξονας είναι λοξά στην ατέρμονη βίδα.
• Ράφι και γρανάζι: είναι ένα σετ γραναζιών που είναι επίσης κοινό σε ορισμένους μηχανισμούς και επιτρέπει σε μια περιστροφική κίνηση ενός άξονα να μετατραπεί σε γραμμική κίνηση ή το αντίστροφο.

Εάν παρευρεθείτε σε Η σύνθεσή του, μπορείτε επίσης να κάνετε διάκριση μεταξύ υλικών όπως:

• ΜέταλλαΣυνήθως κατασκευάζονται από διαφορετικούς τύπους χάλυβα, κράματα χαλκού, κράματα αλουμινίου, χυτοσίδηρο ή γκρι χυτοσίδηρο, κράματα μαγνησίου κ.λπ.
• Πλαστικά είδη: χρησιμοποιείται σε ηλεκτρονικά είδη, παιχνίδια κ.λπ. Πρόκειται για γρανάζια πολυανθρακικού, πολυαμιδίου ή PVC, ρητίνες ακετάλης, πολυαιθεροαιθεροκετόνη PEEK, πολυτετραφθοροαιθυλένιο (PTFE) και πολυμερή υγρών κρυστάλλων (LCP).
• Ξύλο: δεν είναι κοινά, μόνο σε παλιούς μηχανισμούς ή σε ορισμένα παιχνίδια.
• άλλοι: είναι πιθανό ότι για πολύ συγκεκριμένες περιπτώσεις χρησιμοποιούνται άλλες ίνες ή ειδικά υλικά.

Πού να αγοράσετε εργαλεία;

Εσείς βρείτε διαφορετικούς τύπους γραναζιών σε πολλά καταστήματα μηχανικών ή ηλεκτρονικών. Για παράδειγμα, εδώ είναι μερικά παραδείγματα:

• Πλαστικό κιτ εργαλείων. Με 64 διαφορετικούς τύπους.
• Δεν βρέθηκαν προϊόντα.
• Σετ από 16 διαφορετικά μεταλλικά μέρη, συμπεριλαμβανομένων ελικοειδών.
• Πλαστικό κιτ γραναζιών.

Αυτά τα προϊόντα είναι μικρού μεγέθους, εάν χρειάζεστε μεγαλύτερα γρανάζια, είναι πιθανό ότι δεν θα τα βρείτε τόσο εύκολα. Επίσης, εάν χρειάζεστε κάτι πολύ συγκεκριμένο, πολλά εργαστήρια με τορνουά μπορούν φτιάξε το για σένα. ο εκτυπωτές 3D βοηθούν επίσης τους κατασκευαστές να δημιουργήσουν τα δικά τους εργαλεία.

Βασικοί υπολογισμοί για συστήματα γραναζιών

Όπως μπορείτε να δείτε σε αυτό το GIF, πρέπει να καταλάβετε ότι όταν δύο γρανάζια πλέουν, και οι δύο άξονες θα περιστραφεί προς την αντίθετη κατεύθυνση και όχι με την ίδια έννοια. Όπως μπορείτε να δείτε, αν κοιτάξετε την κόκκινη οδοντωτή rue στρέφεται προς τα δεξιά, ενώ η μπλε στρίβει προς τα αριστερά.

Ως εκ τούτου, για έναν άξονα να περιστρέφεται προς την ίδια κατεύθυνση θα ήταν απαραίτητο να προσθέσετε έναν επιπλέον τροχό, όπως τον πράσινο. Με αυτόν τον τρόπο, το κόκκινο και το πράσινο περιστρέφονται προς την ίδια κατεύθυνση. Αυτό συμβαίνει επειδή, καθώς το μπλε περιστρέφεται προς τα αριστερά, όταν εμπλέκεται μπλε-πράσινο, το πράσινο θα αντιστρέψει ξανά την κατεύθυνση περιστροφής, συγχρονίζοντας με το κόκκινο.

Ένα άλλο πράγμα που μπορεί να εκτιμηθεί σε αυτό το GIF είναι ταχύτητα στροφής. Εάν όλα τα γρανάζια είχαν την ίδια διάμετρο και αριθμό δοντιών, όλοι οι άξονες θα περιστρέφονταν με την ίδια ταχύτητα. Από την άλλη πλευρά, όταν αλλάζει ο αριθμός / διάμετρος των δοντιών, η ταχύτητα αλλάζει επίσης. Όπως μπορείτε να δείτε σε αυτήν την περίπτωση, το κόκκινο είναι αυτό που περιστρέφεται ταχύτερα, καθώς έχει μικρότερη διάμετρο, ενώ το μπλε περιστρέφεται με μέση ταχύτητα και το πράσινο είναι αυτό που περιστρέφεται πιο αργά.

Σε απάντηση σε αυτό, Είναι πιθανό να πιστεύουμε ότι το παιχνίδι με τα μεγέθη μπορεί να αλλάξει η ταχύτητα. Έχετε δίκιο, όπως το ποδήλατο μπορεί να το κάνει με τα γρανάζια ή το κιβώτιο ταχυτήτων το κάνει με τις σχέσεις γραναζιών ενός αυτοκινήτου. Και όχι μόνο αυτό, μπορείτε επίσης να κάνετε υπολογισμούς σχετικά με την ταχύτητα στροφής.

Όταν έχετε δύο γρανάζια, ένα μικρό (γρανάζι) και ένα άλλο μεγάλο (τροχός), θα μπορούσαν να συμβούν τα εξής:

• Εάν φανταστούμε ότι ο κινητήρας ή η έλξη εφαρμόζεται στο γρανάζι και ο τροχός κινείται, αν και το γρανάζι περιστρέφεται με υψηλή ταχύτητα, έχοντας μεγαλύτερο τροχό, θα το επιβραδύνει, ενεργώντας ως αναγωγέας. Μόνο αν είχαν το ίδιο μέγεθος (γρανάζι = τροχός) και οι δύο άξονες θα περιστρέφονταν με την ίδια ταχύτητα.
• Από την άλλη πλευρά, αν φανταστούμε ότι είναι ο τροχός που έχει την πρόσφυση και εφαρμόζεται ταχύτητα σε αυτό, ακόμη και αν είναι χαμηλή, το γρανάζι θα γυρίζει πιο γρήγορα, καθώς το μικρό του μέγεθος λειτουργεί ως πολλαπλασιαστής.

Υπολογισμοί μετάδοσης εργαλείων

Μόλις το καταλάβετε, μπορείτε να εκτελέσετε τους υπολογισμούς ενός απλού συστήματος μετάδοσης μεταξύ δύο ταχυτήτων εφαρμόζοντας ο τύπος:

N1 Z1 = N2 Z2

Όπου Z είναι ο αριθμός των δοντιών των γραναζιών 1 και 2 που είναι πλεγμένα και Ν είναι η ταχύτητα περιστροφής των αξόνων σε RPM (περιστροφές ανά λεπτό ή περιστροφές ανά λεπτό). Για παράδειγμα, φανταστείτε ότι στο GIF παραπάνω, για απλοποίηση:

• Κόκκινο (κίνηση) = 4 δόντια και ο κινητήρας εφαρμόζει ταχύτητα περιστροφής στον άξονα 7 στροφών ανά λεπτό.
• Μπλε = 8 δόντια
• Πράσινο = 16 δόντια

Εάν θέλετε να υπολογίσετε τη στροφή σε αυτό το σύστημα, πρέπει πρώτα να υπολογίσετε την ταχύτητα του μπλε:

4 7 = 8 ζ

z = 4 7/8

z = 3.5 σ.α.λ.

Δηλαδή, ο μπλε άξονας θα περιστρέφεται στα 3.5 RPM, κάπως πιο αργός από το 4 RPM του κόκκινου. Εάν θέλετε να υπολογίσετε τη στροφή του πράσινου, τώρα που γνωρίζετε την ταχύτητα του μπλε:

8 3.5 = 16 ζ

z = 8 3.5/16

z = 1.75

Όπως μπορείτε να δείτε, το πράσινο περιστρέφεται στις 1.75 RPM, το οποίο είναι πιο αργό από το μπλε και το πράσινο. Και τι θα συνέβαινε εάν ο κινητήρας βρίσκεται στον πράσινο άξονα και ο κινητήριος τροχός περιστρέφεται στις 4 RPM, τότε η περιστροφή θα είναι 8 RPM για μπλε, 16 RPM για κόκκινο.

Επομένως, όταν ο κινητήριος τροχός είναι μικρός, επιτυγχάνεται χαμηλότερη ταχύτητα στον τελικό άξονα, αλλά μεγαλύτερη δύναμη. Σε περίπτωση που ο μεγάλος τροχός φέρει την πρόσφυση, ο μικρός τροχός επιτυγχάνει μεγαλύτερη ταχύτητα, αλλά λιγότερη δύναμη. Επειδή εκεί δυνάμεις ή ροπή διαφορετικός? Κοιτάξτε αυτόν τον τύπο:

P = Τ ω

Όπου P είναι η ισχύς που μεταδίδεται από τον άξονα σε watt (W), T είναι η ανεπτυγμένη ροπή (Nm), ω η γωνιακή ταχύτητα στην οποία περιστρέφεται ο άξονας (rad / s). Εάν η ισχύς του κινητήρα διατηρηθεί και η ταχύτητα περιστροφής πολλαπλασιαστεί ή μειωθεί, τότε το T. αλλάζει επίσης. Το ίδιο συμβαίνει εάν το T διατηρείται σταθερό και η ταχύτητα μεταβάλλεται, τότε το P αλλάζει.

Ίσως θέλετε επίσης να υπολογίσετε εάν ένας άξονας περιστρέφεται σε X RPM, πόσο θα προχωρούσε γραμμικά, δηλαδή, το γραμμική ταχύτητα. Για παράδειγμα, φανταστείτε ότι στο κόκκινο έχετε έναν κινητήρα DC και στον πράσινο άξονα έχετε τοποθετήσει έναν τροχό έτσι ώστε ένας κινητήρας να κινείται σε μια επιφάνεια. Πόσο γρήγορα θα πήγαινε;

Για να το κάνετε αυτό, πρέπει απλώς να υπολογίσετε την περιφέρεια του ελαστικού που έχετε εγκαταστήσει. Για να το κάνετε αυτό, πολλαπλασιάστε τη διάμετρο με το Pi και θα σας δώσει την περιφέρεια. Γνωρίζοντας πόσο μπορεί να προχωρήσει ο τροχός με κάθε στροφή και λαμβάνοντας υπόψη τι περιστρέφεται κάθε λεπτό, μπορεί να επιτευχθεί η γραμμική ταχύτητα ...

Εδώ σας δείχνω ένα βίντεο για να το καταλάβετε με καλύτερο τρόπο:

Υπολογισμοί για σκουλήκι και γρανάζι

Ως προς γρανάζι και γρανάζι, μπορεί να υπολογιστεί με τον τύπο:

i = 1 / Ζ

Αυτό συμβαίνει επειδή η βίδα θεωρείται σε αυτό το σύστημα ως ένας οδοντωτός τροχός που έχει κοπεί ελικοειδώς. Έτσι, εάν έχετε ένα γρανάζι 60 δοντιών, για παράδειγμα, τότε θα είναι 1/60 (αυτό σημαίνει ότι η βίδα θα πρέπει να περιστραφεί 60 φορές για να ολοκληρώσει το γρανάζι 1 στροφή) Επιπλέον, είναι ένας μηχανισμός που δεν είναι αναστρέψιμος όπως άλλοι, δηλαδή, το γρανάζι δεν μπορεί να περιστραφεί έτσι ώστε το σκουλήκι να περιστρέφεται, μόνο το σκουλήκι μπορεί να είναι ο άξονας μετάδοσης κίνησης εδώ.

Υπολογισμοί Rack και γραναζιών

Για το σύστημα Ράφι και γρανάζι, οι υπολογισμοί αλλάζουν ξανά, στην περίπτωση αυτή είναι:

V = (p Z N) / 60

Δηλαδή, πολλαπλασιάστε το βήμα των οδοντωτών δοντιών (σε μέτρα), με τον αριθμό των οδοντωτών δοντιών και με τον αριθμό των στροφών γραναζιού (σε RPM). Και αυτό διαιρείται με το 60. Για παράδειγμα, φανταστείτε ότι έχετε ένα σύστημα με γρανάζι 30 δοντιών, βήμα 0.025m και ταχύτητα περιστροφής 40 RPM:

V = (0.025) / 30

V = 0.5 m / s

Δηλαδή, θα προχωρούσε μισό μέτρο κάθε δευτερόλεπτο. Και, σε αυτήν την περίπτωση, Ναι είναι αναστρέψιμοΔηλαδή, εάν το ράφι κινείται κατά μήκος, το γρανάζι μπορεί να περιστραφεί.

Θα μπορούσατε ακόμη και να υπολογίσετε πόσο καιρό θα χρειαζόταν για να ταξιδέψετε μια απόσταση λαμβάνοντας υπόψη τον τύπο για ομοιόμορφη γραμμή κίνησης (v = d / t), δηλαδή, εάν η ταχύτητα είναι ίση με την απόσταση διαιρούμενη με το χρόνο, τότε ο χρόνος διαγράφεται:

t = d / v

Επομένως, γνωρίζοντας ήδη την ταχύτητα και την απόσταση που θέλετε να υπολογίσετε, για παράδειγμα, φανταστείτε ότι θέλετε να υπολογίσετε πόσο καιρό θα χρειαζόταν για να διανύσετε 1 μέτρο:

t = 1 / 0.5

t = 2 δευτερόλεπτα

Ελπίζω να σας βοήθησα να αποκτήσετε τουλάχιστον τις πιο βασικές γνώσεις σχετικά με τα γρανάζια, έτσι ώστε να καταλάβετε πώς λειτουργούν και πώς μπορείτε να τα χρησιμοποιήσετε προς όφελός σας στα μελλοντικά σας έργα.