ang Ang mga logic gate ay ang batayan ng digital electronics. Para sa kadahilanang ito, ang mga ito ay napakahalaga, at kung gusto mong magsimulang magtrabaho kasama sila, dapat mong malaman kung ano sila, kung paano sila binubuo, at ang kanilang tungkulin. Kaya maaari mong gamitin ang mga serye ng mga chips na umiiral sa merkado na may ganitong uri ng mga pinto upang maaari mong simulan ang paggawa ng iyong sariling mga proyekto na gumagana sa logic na ito.
Ang mga pintong ito, pinagsama sa iba Mga elektronikong sangkap, at kahit na may mga plato tulad ng Arduino, maaari silang magbigay ng maraming laro sa mga gumagawa tulad ng nakikita mo sa iyong sarili.
Ano ang logic gates?
ang mga gate ng lohika ang mga ito ay mga pangunahing elemento ng digital logic para sa pagpapatupad ng mga digital electronic circuit. Ang mga gate na ito ay nagbibigay ng mababa (0) o mataas (1) na signal ng boltahe sa kanilang output depende sa estado ng kanilang mga input. Sila ay karaniwang may isang labasan at dalawang pasukan, ngunit maaaring may mga pintuan na may higit sa 2 pasukan. Bilang karagdagan, may mga partikularidad tulad ng inverting gate o HINDI, mayroon lamang itong isang input at isang output.
Salamat sa mga Boolean input at output na maaari mong makuha elementarya binary logic operations, tulad ng pagdaragdag, pagpaparami, pag-negasyon, atbp.
Paano sila ipinatupad?
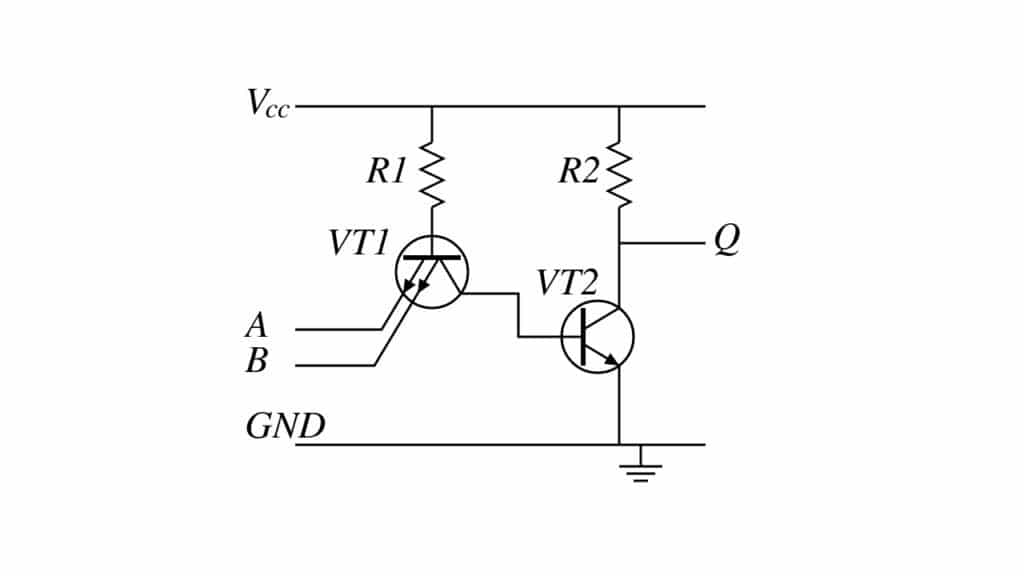
- NAND gate sa TTL
- NAND gate sa CMOS
Logic gate ay hindi lamang maaaring ipatupad sa isang paraan. Sa katunayan, iyon ang dahilan kung bakit may iba't ibang lohikal na pamilya. Ang bawat isa sa mga pamilyang ito ay magpapatupad ng gate sa isang paraan, gamit ang iba't ibang mga elektronikong sangkap.
Por ejemploKung TTL ang gagamitin para sa chip, ang mga gate ay bubuuin ng bipolar transistors, habang ang CMOS logic ay nakabatay lamang sa MOSFET transistors. Bilang karagdagan sa dalawang pamilyang ito, na kadalasang pinakasikat, mayroon ding iba tulad ng BiCMOS (pinagsasama ang bipolar at CMOS transistors), RTL (resistors at bipolar transistors), DTL (diodes at transistors), ECL, IIL, atbp.
Walang isang pamilya na mas mahusay kaysa sa isa pa, ito ay depende sa aplikasyon. Ngunit gayunpaman, CMOS Ito ay isa sa mga pinaka ginagamit sa mga advanced na circuit, tulad ng CPU, MCU, GPU, memory, atbp. Para sa iba pang mas simpleng mga circuit karaniwan din na hanapin ang TTL.
aplikasyon
Ang mga aplikasyon ng mga logic gate na ito ay walang katapusan. Sa mga mahahalagang "brick" na ito maaari kang bumuo maraming mga digital circuit. Mula sa isang simpleng adder, sa isang kumplikadong CPU, sa pamamagitan ng maraming iba pang mga circuit na maaari mong isipin. Sa katunayan, marami sa mga system na ginagamit mo araw-araw, tulad ng iyong PC, iyong TV, mobile, atbp., ay may bilyun-bilyong logic gate.
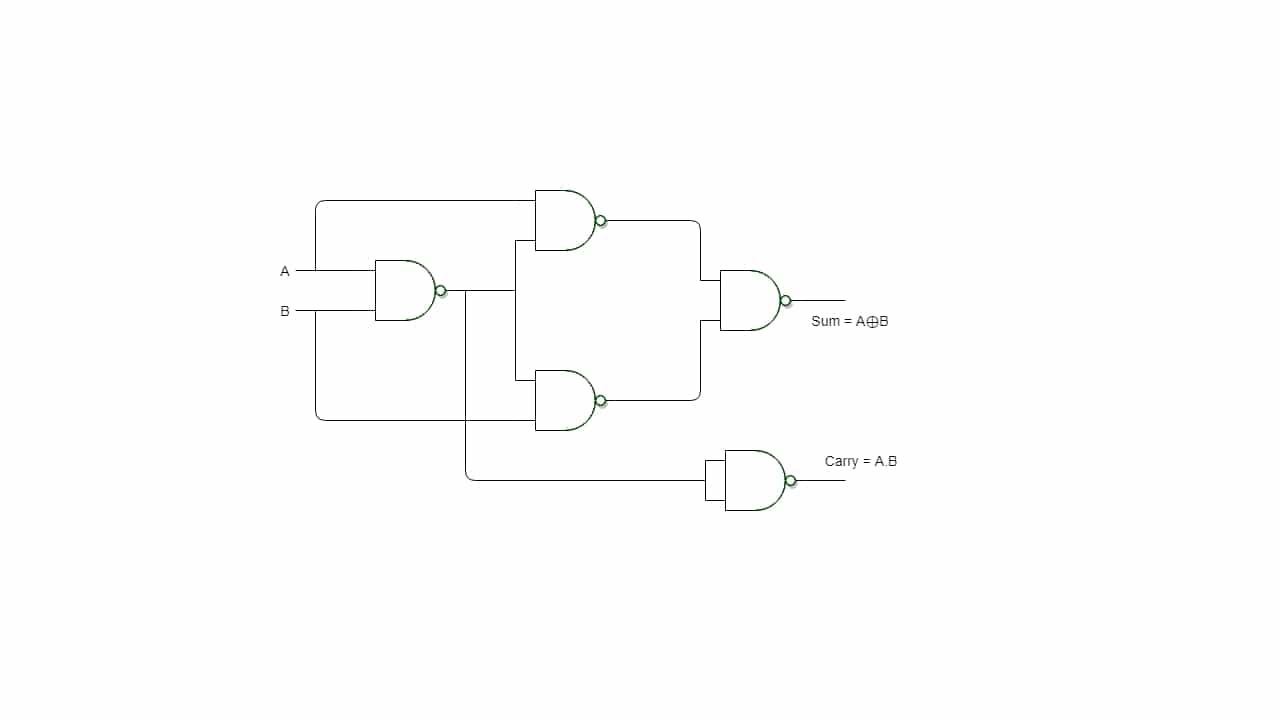
Un praktikal na halimbawa ng application ng logic gate ay ang simpleng adder na makikita mo sa larawan sa itaas. Ito ay isang napaka-simpleng circuit, na may kakayahang magdagdag ng dalawang bits (A at B) sa mga input nito upang maibigay ang resulta ng Sum, at gayundin ang Carry, iyon ay, kung ano ang iyong aalisin ... Makikita mo ang mga resulta na gagawin nito. ibigay sa sumusunod na talahanayan:
| A | B | Kabuuan | Magdala | Binary na resulta |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 00 |
| 0 | 1 | 1 | 0 | 01 |
| 1 | 0 | 1 | 0 | 01 |
| 1 | 1 | 0 | 1 | 10 |
Kung titingnan mo ang talahanayang ito, kung magdadagdag ka ng 0 + 0 sa binary ito ay magbibigay sa iyo ng 0, kung magdadagdag ka ng 1 + 0 ito ay 1, ngunit kung magdagdag ka ng 1 + 1 ay magbibigay ito ng 2, na sa binary system ay tumutugma sa 10.
Mga uri ng mga gate ng lohika
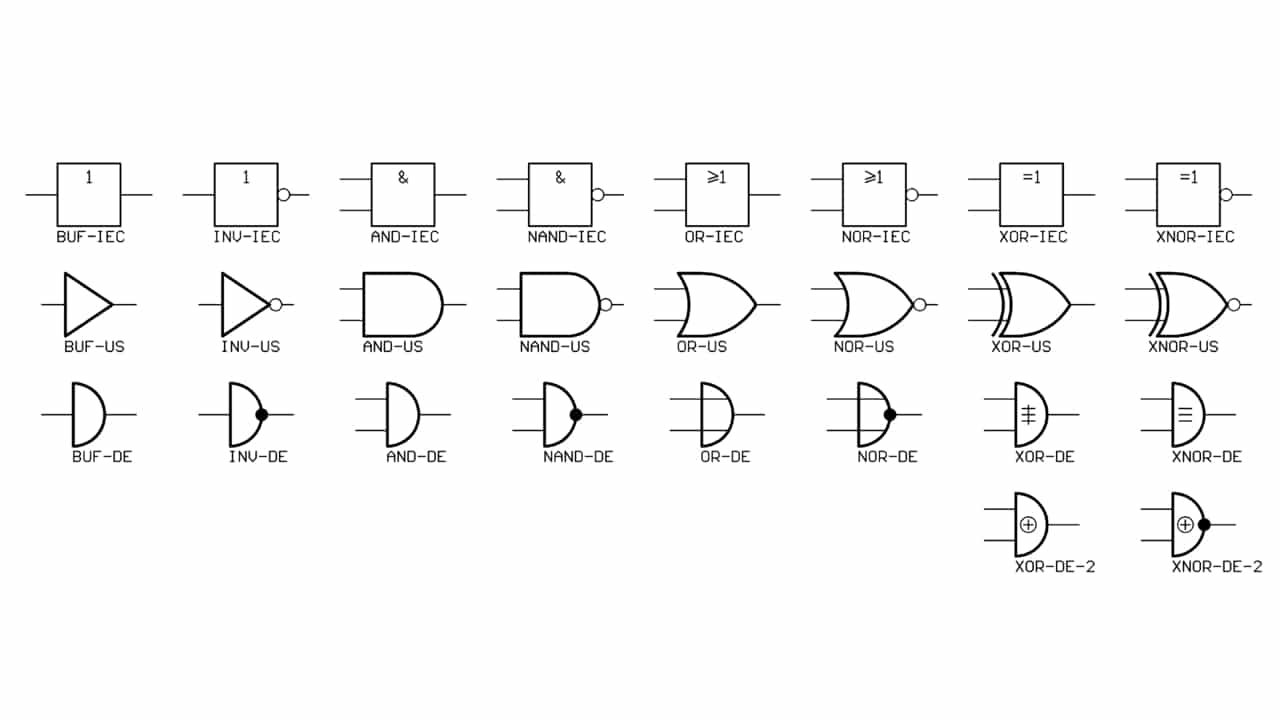
Tulad ng para sa mga uri ng mga gate ng lohika, mayroon kang isang mahusay na bilang ng mga ito, kahit na ang pinaka ginagamit ay ang mga sumusunod (kasama ang kanilang mga talahanayan ng katotohanan):
- Buffer (Oo): ito ay kilala bilang buffer o direktang gate, dahil ang output nito ay magkakaroon ng parehong estado bilang input nito. Kahit na ito ay tila walang silbi, sa maraming logic circuits ito ay madalas na ginagamit bilang isang kasalukuyang amplifier o bilang isang boltahe na tagasunod.
| Pasukan | Salida |
|---|---|
| 0 | 0 |
| 1 | 1 |
- HINDI (inverter): ay ang logical negation (¬ o '), ibig sabihin, binabaligtad nito ang bit sa output nito.
| Pasukan | Salida |
|---|---|
| 0 | 1 |
| 1 | 0 |
- AT (Y): ang ibang gate na ito ay gumaganap ng product function (·) ng mga binary bits ng input nito. Iyon ay, ito ay magiging tulad ng pagpaparami ng A at B. Samakatuwid, ang anumang bagay sa zero ay zero, ito ay magbibigay lamang ng isa sa output nito kung ang parehong mga input ay 1. Kaya't ang pangalan nito ay 1 AT 1.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- ginto): ang isa pang gate na ito ay gumaganap ng isang lohikal na operasyon ng karagdagan (+). Ibig sabihin, Alinman sa isa sa mga output nito O sa isa pa, O pareho ay dapat nasa 1 para maging 1 ang output nito. Kapag pareho ay 0, ang output ay 0 din.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- XOR (o eksklusibo): Ang eksklusibong OR na ito ay gumaganap ng Boolean function na A'B + AB ', at ang simbolo nito ay
. Sa kasong ito, kung ang dalawang input nito ay pantay, ang output ay 0. Kung magkaiba ang mga ito, ito ay magiging 1.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- NAND (Y tinanggihan): ay ang negated na lohikal na produkto, iyon ay, ang kabaligtaran ng AND. Ito ay tulad ng paggamit ng isang HINDI sa AND output upang baligtarin ang output bits. Samakatuwid, ang mga resulta ay:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- NOR (O tinanggihan): ang negated logical sum, o kung ano ang pareho, isang OR kasama ang negated na output nito, na nagreresulta sa kabaligtaran ng OR.
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
- XNOR (eksklusibong NOR): ito ay tulad ng paglalapat ng binary complement sa isang XOR gate. Iyon ay, gawin ang AB + A'B 'operasyon. A beses B idinagdag sa A beses B tinanggihan. Samakatuwid, ang mga output ay magiging katulad ng sa baligtad na XOR:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Parehong NOR at NAND ang dalawa sa pinakakawili-wiling mga gate, dahil kilala sila bilang unibersal na mga pintuan ng lohika. Iyon ay, maaari kang gumawa ng mga circuits lamang sa kanila upang kumatawan sa anumang iba pang uri ng logic gate. Mahalaga ito, dahil kung bibili ka ng mga chips sa mga pintong ito, maaari mong makuha ang lahat ng mga function. Halimbawa, kung ang dalawang input ng isang NOR ay naka-bridge o ang isang NAND ay katumbas ng isang NOT. Mayroon kang higit pang katumbas dito:
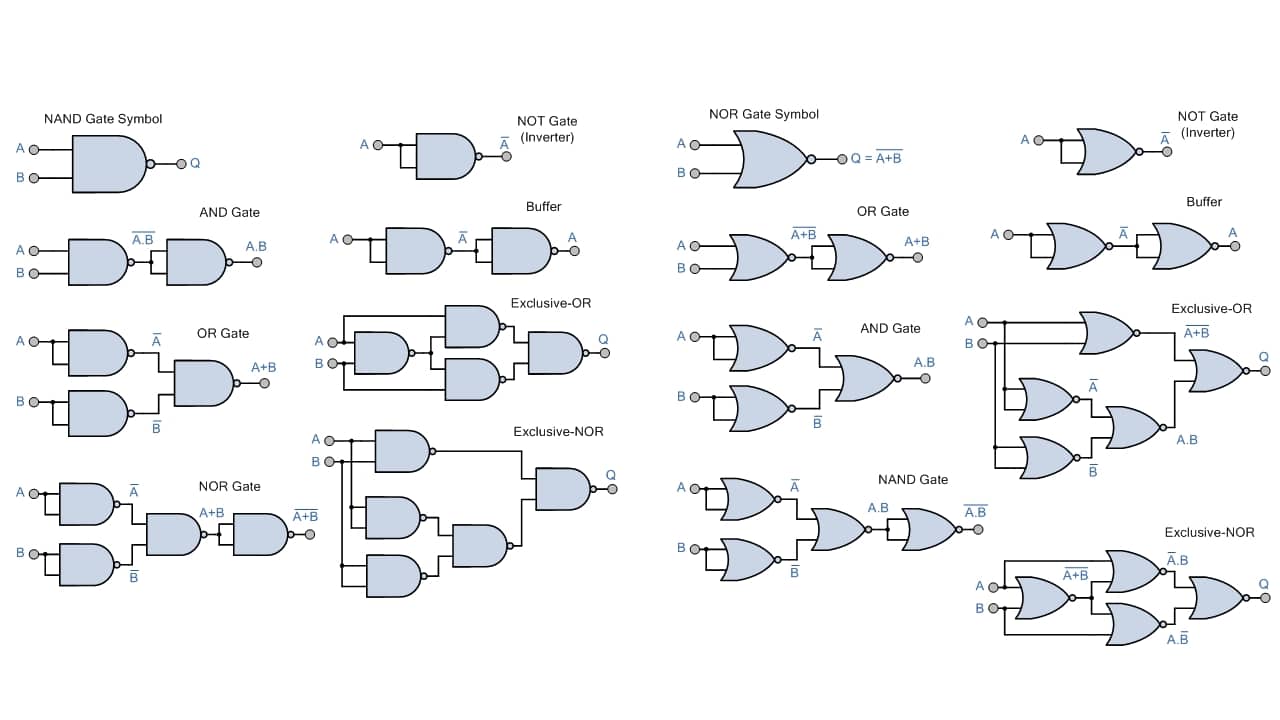
Mga function: electronics-tutorials.ws
Te Payo koUpang matuto nang higit pa, ang Google ay isang simpleng circuit na may anumang mga gate. At upang malaman kung ano ang ginagawa nito, gumawa ng isang uri ng "reverse engineering", sundin ang mga linya ng mga input at output at tingnan ang katayuan ng bawat linya ayon sa mga input na ibinigay sa output.
Por ejemploKung titingnan mo ang imahe sa itaas, ang equivalence diagram ng isang OR na may mga NAND gate, makikita mo na ito ay binubuo ng dalawang NAND gate na ang kanilang output ay naka-bridge at ang parehong mga output ay mapupunta sa isa pang NAND. Isaisip ang sumusunod:
- Kung pupunta ka sa talahanayan ng katotohanan ng NAND, makikita mo na kapag ang dalawang input nito ay 0 ang output ay 1, at kapag ang dalawang input nito ay 1 ang output ay 0.
- Habang sila ay naka-bridge, kung ang input ay 1 (ang isa ay pumapasok sa pareho), ang resulta ay 0. At kapag ang input ay 0 (parehong zero), ang output ay magiging 1, na katumbas ng isang HINDI.
- Samakatuwid, mayroon kaming dalawang HINDI para sa mga bit A at B. Sa kanilang output ay magkakaroon tayo ng A 'at B'.
- Ang dalawang negasyon na iyon ay napupunta sa huling NAND, na gagawa ng isang baligtad na lohikal na produkto ng dalawang bit na iyon.
- Ayon sa mga batas ng lohika, ito ay katumbas ng direktang kabuuan, iyon ay, A + B. Samakatuwid, ang huling resulta ay magiging parang ito ay isang O ...
Serye ng Logic Gate Chip - Saan Bibili
- Logic gate DIP chip
- Panloob na diagram ng chip
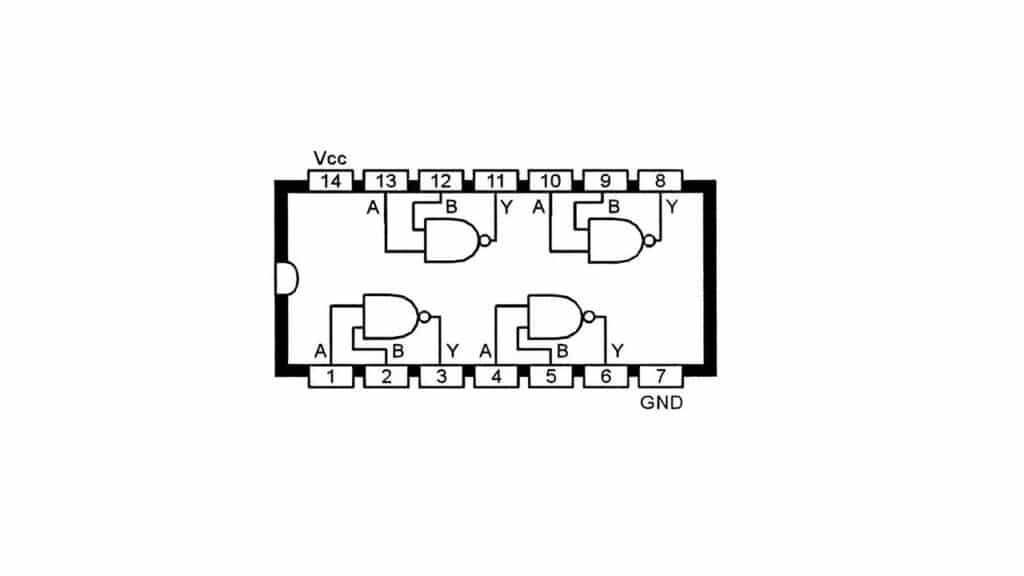
Sa mga tindahan na dalubhasa sa electronics maaari kang bumili ng murang chips na may logic gate upang simulan ang paggamit sa iyong mga proyekto. Ang mga chip na ito ay hindi isang solong logic gate, ngunit pinapayagan ka nitong magkaroon ng ilan sa mga ito upang maiugnay mo ang kanilang mga input at output ayon sa kailangan mo. Halimbawa, sa diagram sa larawan sa itaas makikita mo ang isang tipikal na pinout ng isang DIP chip na may 4 na NAND gate. Bilang karagdagan, mayroon din itong dalawang pin para sa kapangyarihan (Vcc at GND).
Narito ang ilan mga rekomendasyon sa pagbili:
- Walang nahanap na mga produkto.
- Huaban: 30-chip kit na may mga unibersal na NAND gate.
- Zebulon: 120 CMOS chip kit.
Iba pang mga mapagkukunan
Upang matuto nang higit pa tungkol sa kung paano ipatupad ang mga gate na ito at kung paano simulan ang paglikha ng mga circuit sa kanila, maaari mong gamitin ang mga ito. mga otros recursos ano ang inirerekumenda ko:
- SimulIDE software upang magawang gayahin ang pagpapatakbo ng mga circuit na ito na may mga gate. Ito ay libre, open source, at cross-platform.
- Online na binary calculator (Maaari mo ring gamitin ang calculator ng iyong operating system sa binary mode).
- Walang nahanap na mga produkto.
- Digital Logic Circuits Book: mula sa disenyo hanggang sa eksperimento.
Digital logic na may Arduino
Iba pang mapagkukunan ano ang mayroon ka sa iyong mga kamay kung mayroon ka na isang plato Arduino UNO nasa iyong mga kamay ay gumamit ng Arduino IDE upang lumikha ng mga sketch na gayahin ang mga logic function na ito upang, halimbawa, makita ang resulta sa mas visual na paraan gamit ang isang LED na ginagaya ang output ng pinto. Halimbawa, ang paglalagay ng LED sa pin 7 at paggamit ng 8 at 9 bilang mga input A at B:
int pinOut = 7;
int pinA = 8;
int pinB = 9;
void setup()
{
pinMode(pinOut, OUTPUT);
pinMode(pinA, INPUT);
pinMode(pinB, INPUT);
}
void loop()
{
boolean pinAState = digitalRead(pinA);
boolean pinBState = digitalRead(pinB);
boolean pinOutState;
//AND
pinOutState =pinAState & pinBState;
digitalWrite(pinOut, pinOutState);
}
Dito ginamit ang isang AND (&) function, tulad ng nakikita mo, ngunit maaari mong palitan ang linyang iyon ng code sa ilalim ng // AT linya ng iba pang magagamit. iba pang mga function ng lohika:
//OR pinOutState = pinAState | pinBState; //NOT pinOutState = !pinAState; //XOR pinOutState = pinAState ^ pinBState; //NAND pinOutState = !(pinAState & pinBState); //NOR pinOutState = !(pinAState | pinBState); //XNOR pinOutState = !(pinAState ^ pinBState);