
Los engranajes están en multitud de mecanismos actuales, desde relojes analógicos, hasta motores de vehículos, cajas de cambios, pasando por robots, impresoras, y otros muchos sistemas mecatrónicos. Gracias a ellos se pueden realizar sistemas de transmisión e ir más allá de transmitir el movimiento, también pueden alterarlo.
Por eso, son elementos muy importantes que deberías conocer cómo funcionan de forma adecuada. De esa forma, podrás usar los engranajes adecuados para tus proyectos y comprender mejor la forma en la que operan…
¿Qué es un engranaje?
Existen los sistemas de cadenas, los de poleas, las ruedas de fricción, etc. Todos ellos sistemas de transmisión con sus ventajas y desventajas. Pero de todos ellos destaca el sistema de engranajes, que suelen ser los favoritos por sus propiedades:
- Pueden resistir grandes fuerzas debido a sus dientes sin que deslicen, como le podría ocurrir a las ruedas de fricción o poleas.
- Es un sistema reversible, capaz de trasmitir potencia o movimiento en ambos sentidos.
- Permiten un control del movimiento muy preciso, como se puede comprobar en los motores paso a paso, por ejemplo.
- Permiten crear sistemas de transmisión compactos frente a las cadenas o poleas.
- Se pueden combinar diferentes tamaños para interferir en el giro de cada eje. Por lo general, cuando se emplean dos ruedas dentadas, al engranaje más grande se le llama rueda y al pequeño piñón.
Un engranaje o rueda dentada no es más que un tipo de rueda con una serie de dientes tallados en su borde externo o interno, dependiendo del tipo de engranaje que sea. Estas ruedas dentadas estarán en movimiento rotatorio para generar una torsión en los ejes a los que están unidas, y se pueden agrupar para generar sistemas de engranajes más complejos, encajando sus dientes.
Evidentemente, para que eso sea posible, el tipo y tamaño de los dientes debe coincidir. De lo contrario serán incompatibles y no encajarían. Estos parámetros son los que se tratan en el próximo apartado…
Partes de un engranaje
Para que dos engranajes encaje entre sí, se podría variar el diámetro y cantidad de dientes, pero deben respetar una serie de factores que son los que hacen que el engranaje sea compatible entre sí, como el tipo de diente que usan, las dimensiones, etc.
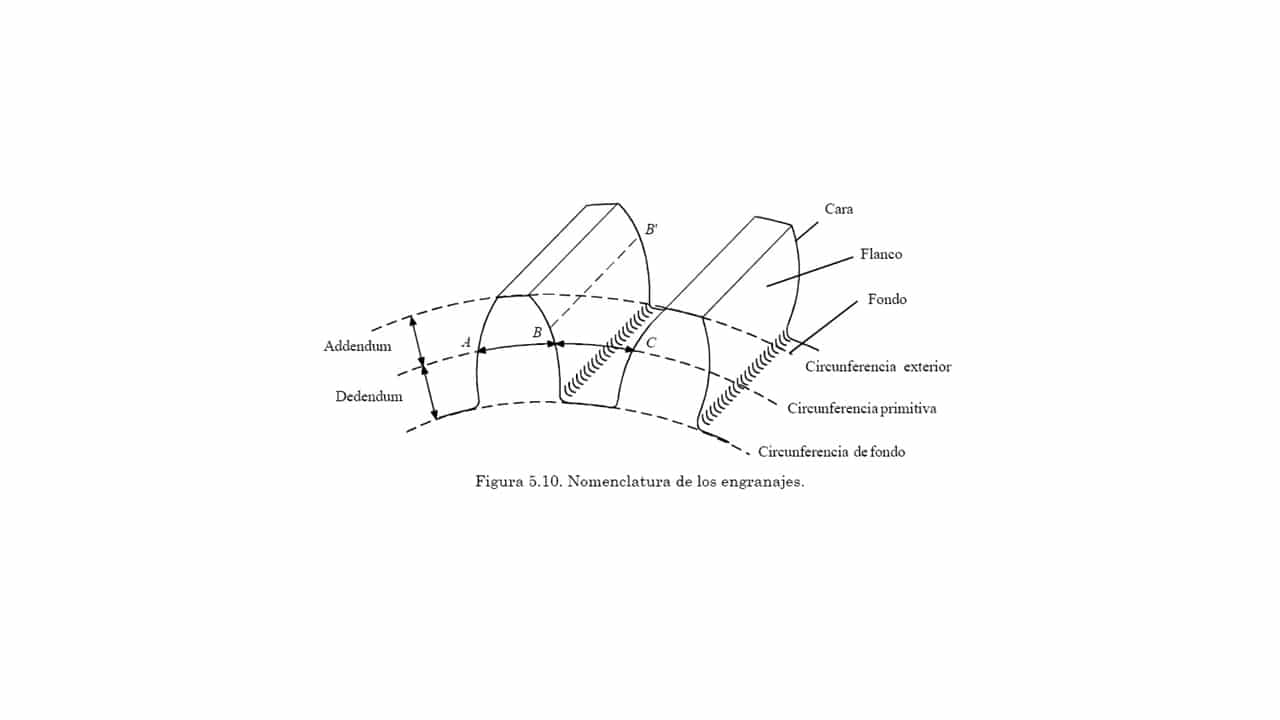
Como puedes ver en la imagen anterior, existen varias partes en un engranaje que deberías conocer:
- Tabique o brazos: es la parte que se encarga de unir la corona y el cubo para poder transmitir el movimiento. Pueden ser más o menos gruesos, y de ello y su composición dependerá en gran medida la resistencia y peso. A veces se suelen agujerear par reducir el peso, otras se opta por un tabique sólido.
- Cubo: es la parte donde se acopla el eje de transmisión del movimiento y que va unido al tabique.
- Corona: es la zona del engranaje donde se han tallado los dientes. Es la más importante, ya que de ella dependerá la compatibilidad, comportamiento y prestaciones del engranaje.
- Diente: es uno de los dientes o protuberancias de la corona. El diente puede subdividirse en varias partes:
- Cresta: es la parte exterior o punta del diente.
- Cara y flanco: es la parte superior e inferior del lateral del diente, es decir, la superficie de contacto entre dos ruedas dentadas que engranan.
- Valle: es la parte inferior del diente o zona intermedia entre dos dientes, donde irá alojada la cresta de otra rueda dentada con la que se engrane.
Todo esto genera una serie de geometrías de corona que distinguirán los tipos y propiedades de los engranajes:
- Circunferencia raíz: marca el valle o fondo de los dientes. Es decir, delimita el diámetro interior del engranaje.
- Circunferencia primitiva: establece la división entre las dos partes del lateral del diente: cara y flanco. Es un parámetro muy importante, ya que en función de ella se definen todas las demás. Dividirá el diente en dos partes, el dedendum y el addendum.
- Pie del diente o dedendum: es la zona inferior del diente que queda entre la circunferencia primitiva y la circunferencia raíz.
- Cabeza del diente o addendum: zona superior del diente, que va desde la circunferencia primitiva y la exterior.
- Circunferencia de cabeza: marcará la cresta de los dientes, es decir, el diámetro exterior del engranaje.
Como puedes imaginar, en función de la corona, diámetro y tipos de dientes, se puede variar el engranaje según:
- Número de dientes: definirá la relación del engranaje y es uno de los parámetros más determinantes para determinar su comportamiento en un sistema de transmisión.
- Altura del diente: la altura total, desde el valle hasta la cresta.
- Paso circular: distancia entre una parte del diente y la misma parte del siguiente diente. Es decir, cuán separados están los dientes, lo que está también relacionado con el número.
- Espesor: es el grosor que tiene el engranaje.
Aplicaciones de los engranajes
Las aplicaciones de los engranajes son muchas, como ya he comentado anteriormente. Algunas de sus aplicaciones prácticas son:
- Cajas de cambios de vehículos.
- Motores paso a paso para el control del giro.
- Bombas hidráulicas.
- Motores de todo tipo, como elementos de transmisión de giro o movimiento.
- Mecanismos diferencial.
- Impresoras para mover los cabezales o rodillos.
- Robots para las partes móviles.
- Maquinaria industrial.
- Relojes analógicos.
- Electrodomésticos con partes mecánicas.
- Dispositivos electrónicos con partes móviles.
- Motores de apertura de puertas.
- Juguetes móviles.
- Maquinaria agrícola.
- Aeronáutica.
- Producción de energía (eólica, térmica,…).
- etc.
Tú puedes pensar multitud de aplicaciones más para tus proyectos con Arduino, robots, etc. Podrás automatizar muchos mecanismos y jugar con las velocidades, etc.
Tipos de engranajes
Según sus dientes y de las características del propio engranaje tienes diferentes tipos de engranajes a tu alcance, cada uno con sus ventajas y desventajas, por lo que es importante elegir el adecuado para cada aplicación.
Los tipos más habituales son:
- Cilíndricos: se usan para eje paralelos.
- Rectos: son los más habituales, usados cuando se necesita un engranaje simple con velocidades no muy elevadas.
- Helicoidal: son una versión algo más avanzada de los anteriores. En ellos los dientes están dispuestos en trayectorias de hélices paralelas alrededor de un cilindro (simples o dobles). Tienen una clara ventaja frente a los rectos, como ser más silenciosos, operar a más altas velocidades, pueden transmitir más potencia, tienen un movimiento más uniforme y seguro.
- Cónicos: se usan para transmitir movimiento entre ejes colocados a diferentes ángulos, incluso a 90º.
- Rectos: usan dientes rectos y comparten características con los cilíndricos rectos.
- En espiral: en este caso soportan mayores velocidades y fuerzas, como le ocurría a los helicoidales.
- Engranaje interno: en vez de tener los dientes o corona tallada por fuera la tienen en su cara interna. No son tan habituales, pero también se utilizan para ciertas aplicaciones.
- Planetarios: es un conjunto de engranajes empleado en ciertos sistemas de transmisión donde hay un engranaje central alrededor del cual giran otros más pequeños. Por eso tiene ese nombre, ya que parecen estar orbitando.
- Tornillo sin fin: es un engranaje habitual en algunos mecanismos industriales o electrónicos. Emplea un engranaje cuyos dientes están tallados en forma de espiral. Generan una velocidad muy constante y sin vibraciones ni ruido. Pueden transmitir a una rueda dentada recta cuyo eje se encuentre en oblicuo al tornillo sin fin.
- Cremallera y piñón: es un conjunto de engranajes también habitual en algunos mecanismos y que permite transformar un movimiento rotatorio de un eje en un movimiento lineal o viceversa.
Si se atiende a su composición, también se puede diferenciar entre materiales como:
- Metales: suelen ser de diferentes tipos de acero, aleaciones de cobre, aleaciones de aluminio, hierro fundido o fundición gris, aleaciones de magnesio, etc.
- Plásticos: se emplean en electrónica, juguetes, etc. Son engranajes de policarbonato, poliamida o PVC, resinas acetálicas, polieteretercetona PEEK, politetrafluoroetileno (PTFE), y polímeros de cristal líquido (LCP).
- Madera: no son habituales, solo en mecanismos antiguos o en ciertos juguetes.
- Otros: es probable que para casos muy concretos se empleen otras fibras o materiales concretos.
¿Dónde comprar engranajes?
Puedes encontrar diferentes tipos de engranajes en multitud de tiendas de mecánica o electrónica. Por ejemplo, aquí tienes algunos ejemplos:
- Kit de engranajes de motor de plástico. Con 64 tipos diferentes.
- No products found.
- Kit de 16 piezas de metal diferentes, incluidos helicoidales.
- Kit de engranajes de husillo de plástico.
Estos productos son de pequeño tamaño, si necesitas engranajes de mayor tamaño es probable que no los encuentres tan fácilmente. Además, si necesitas algo muy específico, muchos talleres de torneros pueden fabricarlo para ti. Las impresoras 3D también están contribuyendo a que los makers puedan crear sus propios engranajes.
Cálculos básicos para los sistemas de ruedas dentadas
Como puedes ver en este GIF, hay que comprender que cuando dos engranajes se engranan, ambos ejes girarán en sentido contrario y no en el mismo sentido. Como ves, si observas la ruda dentada roja está girando hacia la derecha, mientras la azul está haciéndolo a la izquierda.
Por tanto, para que un eje gire en la misma dirección habría que agregar otra rueda adicional, como la verde. De esa forma, rojo y verde giran en la misma dirección. Eso es debido a que, como azul giraba hacia la izquierda, al engranar azul-verde, verde volverá a invertir el sentido del giro, sincronizándose con rojo.
Otra de las cosas que se aprecian en ese GIF es la velocidad de giro. Si todos los engranajes tuviesen el mismo diámetro y número de dientes, todos los ejes estarían rotando a igual velocidad. En cambio, cuando se altera el número de diente/diámetro, también se altera la velocidad. Como puedes ver en este caso, rojo es la que gira más rápido, al tener menor diámetro, mientras que azul gira a una velocidad media y verde es la que más lento gira.
Atendiendo a esto, se puede pensar que jugando con los tamaños se pueden alterar las velocidades. Estás en lo cierto, igual que una bicicleta puede hacerlo con los cambios de marchas o la caja de cambios lo hace con las relaciones de marchas de un coche. Y no solo eso, también se pueden hacer cálculos sobre la velocidad de giro.
Cuando tienes dos engranajes engranados, uno pequeño (piñón) y otro grande (rueda), podría ocurrir lo siguiente:
- Si imaginamos que el motor o tracción se aplica al piñón y la rueda es arrastrada, aunque el piñón gire a alta velocidad, al tener una rueda más grande, ésta lo hará más lento, actuando como un reductor. Solo si fuesen de igual tamaño (piñón=rueda) girarían ambos ejes en la misma velocidad.
- En cambio, si imaginamos que es la rueda la que tiene la tracción y se le aplica una velocidad, aunque sea baja, el piñón estará girando más rápido, ya que su reducido tamaño actúa como multiplicador.
Cálculos de transmisión entre engranajes
Una vez has comprendido esto, se pueden realizar los cálculos de un sistema de transmisión simple entre dos engranajes aplicando la fórmula:
N1 · Z1 = N2 · Z2
Siendo Z el número de dientes de los engranajes 1 y 2 que hay engranados y N es la velocidad de giro de los ejes en RPM (revoluciones por minuto o vueltas por minuto). Por ejemplo, imagina que en el GIF anterior, para simplificar:
- Rojo (tracción) = 4 dientes y el motor está aplicando una velocidad de giro a su eje de 7 RPM.
- Azul = 8 dientes
- Verde = 16 dientes
Si se quisiera calcular el giro en este sistema, primero se debe calcular la velocidad del azul:
4 · 7 = 8 · z
z = 4 · 7 / 8
z = 3.5 RPM
Es decir, el eje azul estaría girando a 3.5 RPM, algo más lenta que las 4 RPM del rojo. Si quisieras calcular el giro de verde, ahora que ya conoces la velocidad de azul:
8 · 3.5 = 16 · z
z = 8 · 3.5 / 16
z = 1.75
Como puedes ver, verde giraría a 1.75 RPM, lo cual es más lento que azul y verde. ¿Y qué pasaría si el motor está situado en el eje de verde y es la rueda tractora girando a 4 RPM, pues entonces el giro sería de 8 RPM para azul, 16 RPM para rojo.
Se deduce así que, cuando la rueda de tracción es pequeña, en el eje final se consigue una velocidad menor, pero mayor fuerza. En el caso de que sea la rueda grande la que lleva la tracción, se consigue en la pequeña una mayor velocidad, pero menor fuerza. ¿Por qué hay potencias o par de giro diferentes? Observa esta fórmula:
P = T · ω
Siendo P la potencia transmitida por el eje en vatios (W), T el par de fuerzas desarrollado (N·m), ω la velocidad angular a la que gira el eje (rad/s). Si se mantiene la potencia del motor y se multiplica o reduce la velocidad de giro, entonces se altera también T. Lo mismo ocurre si se mantiene T constante y se varía la velocidad, entonces P se altera.
Es probable que también quieras calcular si un eje gira a X RPM, cuánto avanzaría linealmente, es decir, la velocidad lineal. Por ejemplo, imagina que en el rojo tienes un motor DC y en el eje verde has colocado una rueda para que un motor se desplace por una superficie. ¿A qué velocidad iría avanzaría?
Para ello, solo tienes que calcular la circunferencia del neumático que has instalado. Para ello, multiplica el diámetro por Pi y te dará la circunferencia. Conociendo lo que puede avanzar con cada giro la rueda y teniendo en cuenta lo que gira cada minuto, se puede obtener la velocidad lineal…
Aquí te muestro un vídeo para que puedas entender esto de una mejor forma:
Cálculos para tornillo sinfín y rueda dentada
En cuanto al tornillo sinfín y la rueda dentada, se puede calcular con la fórmula:
i = 1/Z
Eso es así porque el tornillo se considera en este sistema como una rueda dentada de un solo diente que ha sido tallada de forma helicoidal. Por eso, si tienes una rueda dentada de 60 dientes, por ejemplo, entonces será 1/60 (esto quiere decir que el tornillo debería girar 60 veces para que la rueda dentada complete 1 solo giro). Además, es un mecanismo que no es reversible como otros, es decir, la rueda dentada no se puede girar para que gire el tornillo sinfín, solo el tornillo sinfín puede ser el eje tractor aquí.
Cálculos para piñón y cremallera
Para el sistema de piñón y cremallera, los cálculos vuelven a variar, en este caso son:
V = (p · Z · N) / 60
Es decir, multiplicar el paso de los dientes del piñón (en metros), por el número de dientes del piñón, y por el número de giros del piñón (en RPM). Y eso se divide entre 60. Por ejemplo, imagina que tienes un sistema con un piñón de 30 dientes, un paso de 0.025 m, y una velocidad de giro de 40 RPM:
V = (0.025 · 30 · 40) / 60
V =0.5 m/s
Es decir, avanzaría medio metro cada segundo. Y, en este caso, sí que es reversible, es decir, si se mueve longitudinalmente la cremallera se puede hacer que gire el piñón.
Incluso podrías calcular cuánto tardaría en recorrer una distancia teniendo en cuenta la fórmula de movimiento rectilíneo uniforme (v=d/t), es decir, que si la velocidad es igual a la distancia partido por el tiempo, entonces se despeja el tiempo:
t = d/v
Por tanto, conociendo ya la velocidad y la distancia que quieres calcular, por ejemplo, imagina que deseas calcular cuánto tardaría en recorrer 1 metro:
t = 1/0.5
t = 2 segundos
Espero haberte ayudado a obtener al menos los conocimientos más esenciales sobre los engranajes, para que comprendas cómo funcionan y cómo los puedes usar a tu favor en tus futuros proyectos.



Para un maker como yo (felizmente jubilado) es fabuloso disponer de una información clara, concisa y completa de cómo diseñar engranajes y poder imprimirlos. Enhorabuena