Las puertas lógicas son la base de la electrónica digital. Por esto, son muy importantes, y si quieres comenzar a trabajar con ellas deberías conocer qué son, cómo están constituidas, y su función. Así podrás emplear las series de chips que existen en el mercado que tienen este tipo de puertas para que comiences a hacer tus propios proyectos trabajando con esta lógica.
Estas puertas, combinadas con otros componentes electrónicos, e incluso con placas como Arduino, pueden dar mucho juego a los makers como podrás comprobar tú mismo.
¿Qué son las puertas lógicas?
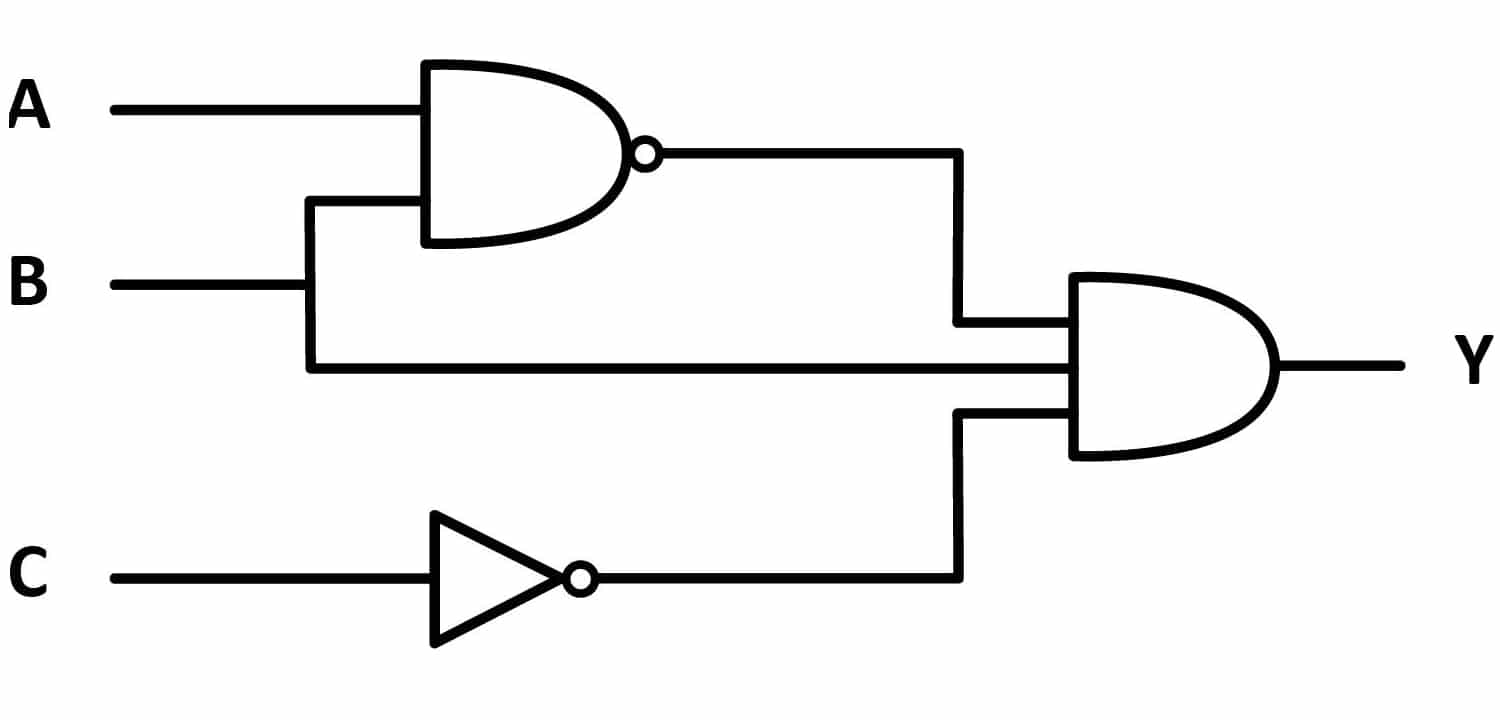
Las puertas lógicas son elementos fundamentales de la lógica digital para la implementación de circuitos electrónicos digitales. Estas puertas otorgan señales de voltaje bajo (0) o alto (1) en su salida según el estado de sus entradas. Generalmente tienen una salida y dos entradas, pero puede haber puertas con más de 2 entradas. Además, hay particularidades como la puerta inversora o NOT, tiene una sola entrada y una salida.
Gracias a esas entradas y salidas booleanas se puede obtener operaciones lógicas binarias elementales, como la suma, la multiplicación, la negación, etc.
¿Cómo se implementan?
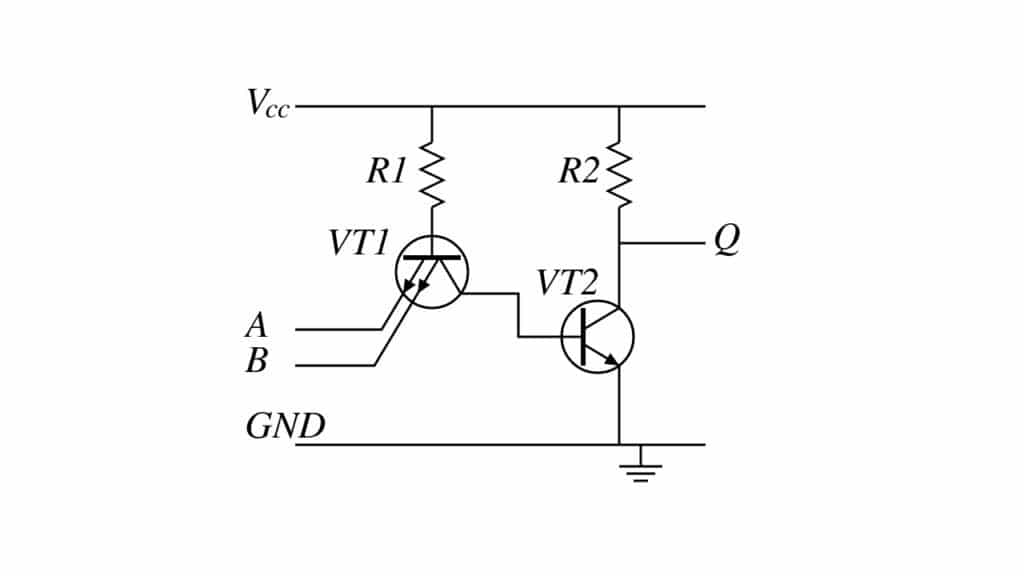
- Puerta NAND en TTL
- Puerta NAND en CMOS
Las puertas lógicas no solo se pueden implementar de una única forma. De hecho, por eso existen diferentes familias lógicas. Cada una de estas familias implementará la puerta de una forma, usando unos componentes electrónicos diferentes.
Por ejemplo, si se emplea TTL para el chip, las puertas estarán formadas por transistores bipolares, mientras que la lógica CMOS se basa únicamente en transistores MOSFET. Además de estas dos familias, que suelen ser las más populares, también existen otras como BiCMOS (combina transistores bipolares y CMOS), RTL (resistencias y transistores bipolares), DTL (diodos y transistores), ECL, IIL, etc.
No existe una familia mucho mejor que otra, dependerá de la aplicación. Sin embargo, la CMOS es una de las más usadas en circuitos avanzados, como la CPU, MCU, GPU, memorias, etc. Para otros circuitos más simples también es frecuente encontrarse con la TTL.
Aplicaciones
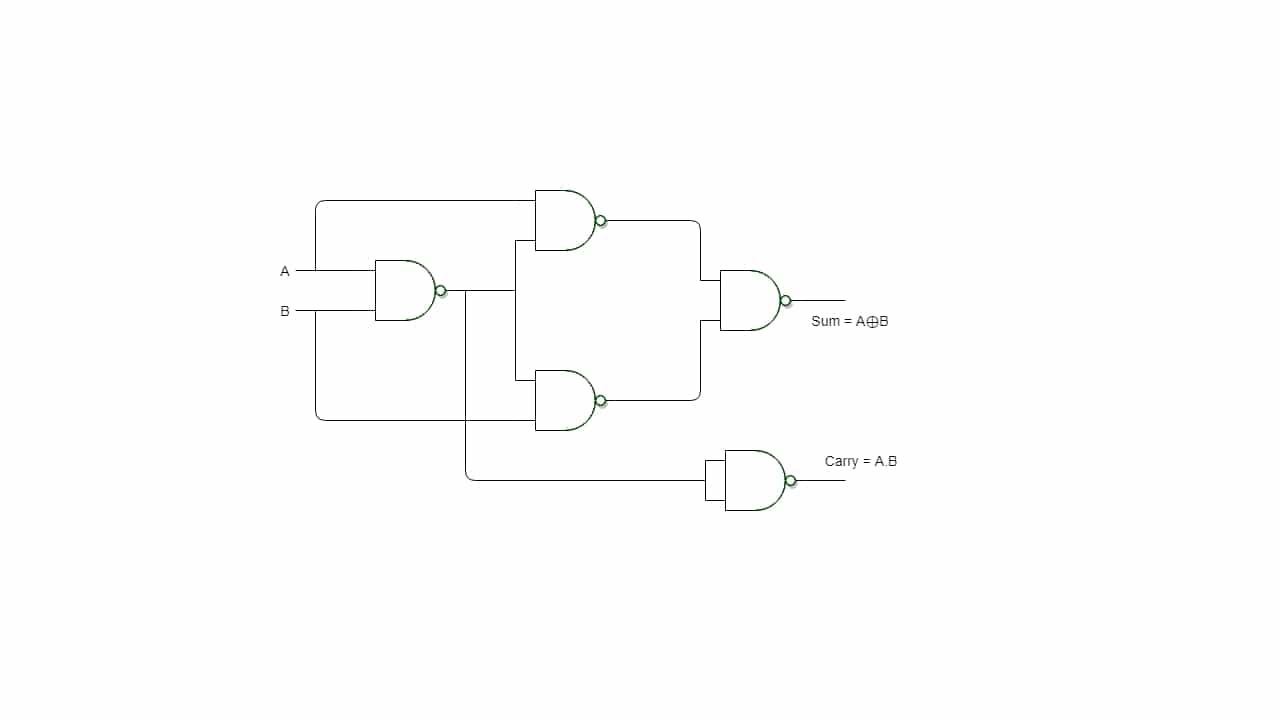
Las aplicaciones de estas puertas lógicas son infinitas. Con estos «ladrillos» esenciales se puede construir multitud de circuitos digitales. Desde un simple sumador, hasta una compleja CPU, pasando por otros muchos circuitos que puedas imaginar. De hecho, muchos de sistemas que usas a diario, como tu PC, tu TV, móvil, etc., tienen miles de millones de puertas lógicas.
Un ejemplo práctico de aplicación de puertas lógicas sería este sencillo sumador que puedes ver en la imagen superior. Se trata de un circuito muy sencillo, que es capaz de sumar dos bits (A y B) en sus entradas para dar el resultado Sum, y también el Carry, es decir, lo que te llevas… Puedes ver los resultados que daría en la siguiente tabla:
| A | B | Sum | Carry | Resultado binario |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 00 |
| 0 | 1 | 1 | 0 | 01 |
| 1 | 0 | 1 | 0 | 01 |
| 1 | 1 | 0 | 1 | 10 |
Si te fijas en esta tabla, si sumas 0+0 en binario te da 0, si sumas 1+0 es 1, pero si sumas 1+1 daría 2, que en sistema binario corresponde a 10.
Tipos de puertas lógicas
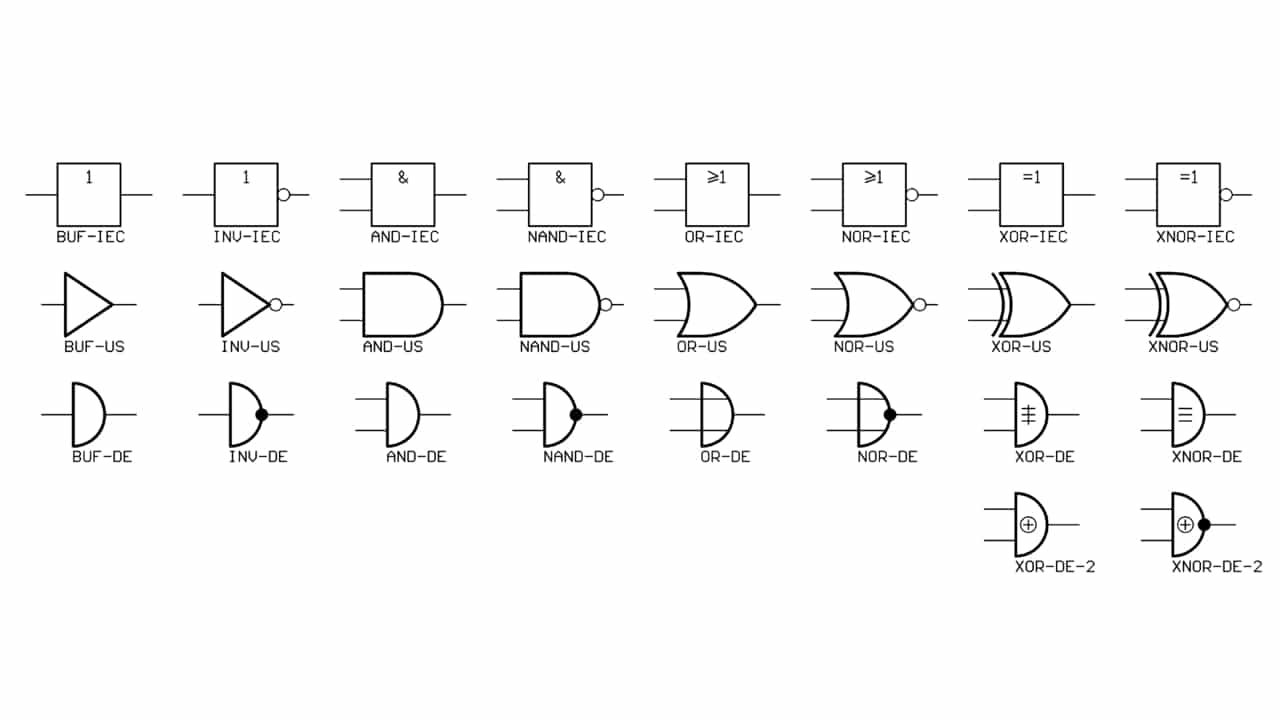
En cuanto a los tipos de puertas lógicas, tienes un buen número de ellas, aunque las más usadas son las siguientes (con sus tablas de verdad):
- Buffer (Sí): se conoce como buffer o puerta directa, ya que su salida tendrá el mismo estado que su entrada. Aunque parezca que carece de utilidad, en muchos circuitos lógicos se suele usar como un amplificador de la corriente o como un seguidor de tensión.
| Entrada | Salida |
|---|---|
| 0 | 0 |
| 1 | 1 |
- NOT (inversor): es la negación lógica (¬ o ‘), es decir, invierte el bit a su salida.
| Entrada | Salida |
|---|---|
| 0 | 1 |
| 1 | 0 |
- AND (Y): esta otra puerta realiza una función producto (·) de los bits binarios de su entrada. Es decir, sería como multiplicar A y B. Por tanto, cualquier cosa por cero es cero, tan solo daría uno a su salida si ambas entradas son 1. De ahí su nombre 1 Y 1.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- OR (O): esta otra puerta realiza una operación de suma lógica (+). Es decir, O una de sus salidas O la otra, O ambas deben estar a 1 para que su salida sea 1. Cuando ambas son 0, la salida es 0 también.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- XOR (O exclusiva): esta O exclusiva realiza la función booleana A’B+AB’, y su símbolo es . En este caso, si sus dos entradas son iguales, la salida es 0. Si son distintas, entonces será 1.
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- NAND (Y negada): es el producto lógico negado, es decir, el inverso de la AND. Es como si usases una NOT en la salida de la AND para invertir los bits de salida. Por tanto, los resultados son:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- NOR (O negada): la suma lógica negada, o lo que es lo mismo, una OR con su salida negada, dando como resultado lo inverso de la OR.
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
- XNOR (NOR exclusiva): es como aplicar el complemento binario a una puerta XOR. Es decir, realizar la operación AB + A’B’. A por B sumado a A por B negadas. Por tanto, las salidas serán como las de la XOR invertidas:
| A | B | S |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tanto la NOR como la NAND son dos de las puertas más interesantes, ya que se conocen como puertas lógicas universales. Es decir, se pueden hacer circuitos solo con ellas para representar cualquier otro tipo de puerta lógica. Esto es importante, puesto que si compras chips con estas puertas, podrás tener todas las funciones. Por ejemplo, si se puentean las dos entradas de una NOR o una NAND equivale a una NOT. Más equivalentes los tienes aquí:
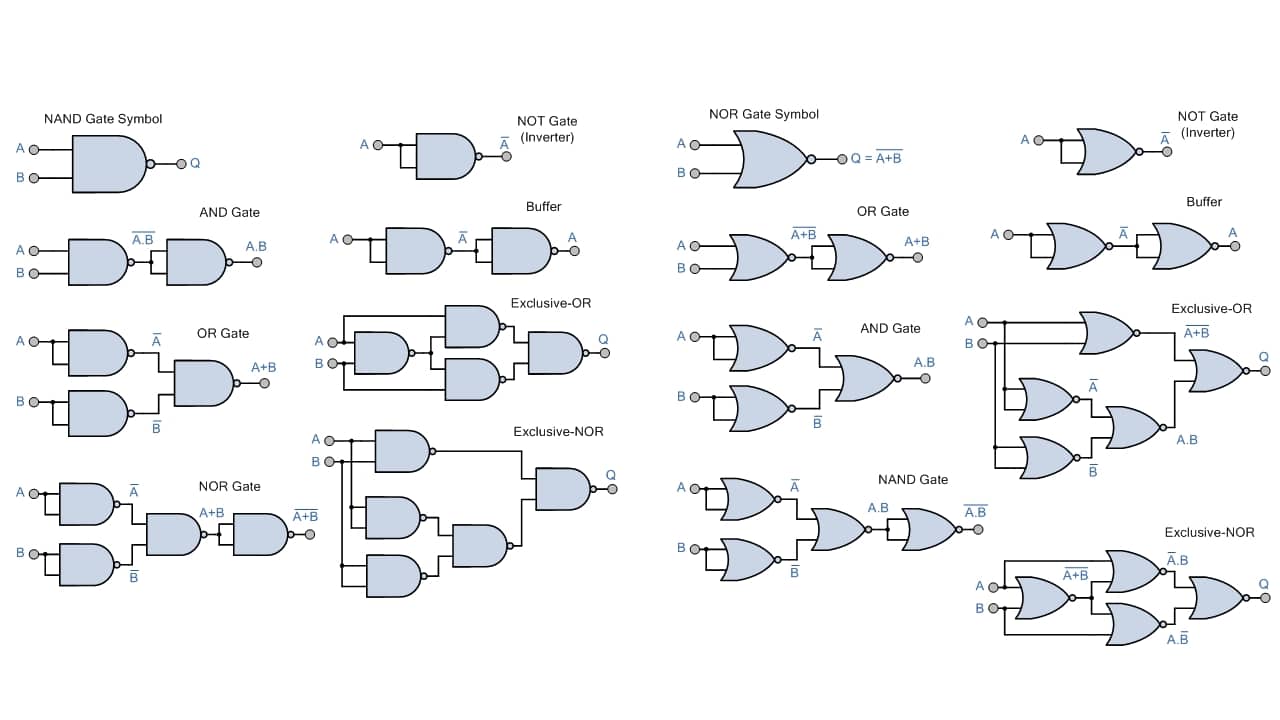
Funciones: electronics-tutorials.ws
Te aconsejo, para aprender más, que busques en Google un circuito simple con puertas cualquiera. Y para saber qué hace, hacer una especie de «ingeniería inversa», sigas las líneas de las entradas y salidas y vayas viendo el estado de cada línea según unas entradas dadas hasta la salida.
Por ejemplo, si te fijas en la imagen superior, el diagrama de equivalencia de una OR con puertas NAND, verás que se compone de dos puertas NAND con su salida puenteada y ambas salidas van a otra NAND. Ten en cuenta lo siguiente:
- Si te vas a la tabla de verdad de la NAND, verás que cuando sus dos entradas son 0 la salida es 1, y cuando sus dos entradas son 1 la salida es 0.
- Al estar puenteadas, si la entrada es 1 (entra uno por ambas), el resultado es 0. Y cuando la entrada está a 0 (ambas a cero), la salida será 1, lo que equivale a una NOT.
- Por tanto, tenemos dos NOT para los bits A y B. A su salida tendremos por tanto A’ y B’.
- Esas dos negaciones entran en la NAND última, que realizará un producto lógico inverso de esos dos bits.
- Según las leyes de la lógica, esto equivale a la suma directa, es decir, A+B. Por tanto, el resultado final será como si de una OR se tratase…
Series de chips de puertas lógicas: dónde comprar
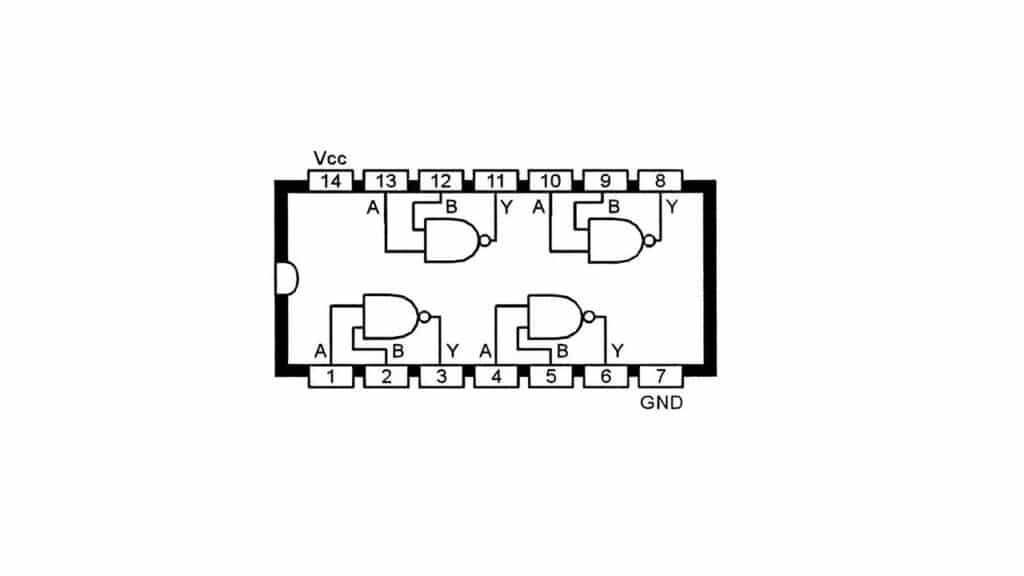
- Chip DIP de puertas lógicas
- Diagrama interno del chip
En las tiendas especializadas en electrónica podrás comprar chips baratos con puertas lógicas para comenzar a usar en tus proyectos. Estos chips no son una única puerta lógica, sino que te permiten disponer de varias de ellas para que puedas enlazar sus entradas y salidas como necesites. Por ejemplo, en el diagrama de la imagen de arriba puedes ver un típico pinout de un chip DIP con 4 puertas NAND. Además, también dispone de dos pines para alimentación (Vcc y GND).
Aquí tienes algunas recomendaciones de compra:
- No products found..
- Huaban: kit de 30 chips con puertas universales tipo NAND.
- Zebulon: kit de 120 chips CMOS.
Otros recursos
Para poder aprender más sobre cómo implementar estas puertas y cómo comenzar a crear circuitos con ellas, puedes hacer uso de estos otros recursos que te recomiendo:
- Software SimulIDE para poder simular el funcionamiento de estos circuitos con puertas. Es gratuito, de código abierto, y multiplataforma.
- Calculadora binaria online (también puedes usar la calculadora de tu sistema operativo en modo binario).
- No products found..
- Libro Circuitos Lógicos Digitales: del diseño al experimento.
Lógica digital con Arduino

Otro recurso que tienes en tus manos si ya tienes una placa Arduino UNO en tus manos es usar Arduino IDE para crear sketchs que simulen estas funciones lógicas para, por ejemplo, ver el resultado de una forma más visual con un LED que simule la salida de la puerta. Por ejemplo, poniendo un LED en el pin 7 y usar 8 y 9 como entradas A y B:
int pinOut = 7;
int pinA = 8;
int pinB = 9;
void setup()
{
pinMode(pinOut, OUTPUT);
pinMode(pinA, INPUT);
pinMode(pinB, INPUT);
}
void loop()
{
boolean pinAState = digitalRead(pinA);
boolean pinBState = digitalRead(pinB);
boolean pinOutState;
//AND
pinOutState =pinAState & pinBState;
digitalWrite(pinOut, pinOutState);
}
Aquí se ha empleado una función AND (&), como puedes ver, pero puedes sustituir esa línea de código bajo la línea //AND por otras para emplear otras funciones lógicas:
//OR pinOutState = pinAState | pinBState; //NOT pinOutState = !pinAState; //XOR pinOutState = pinAState ^ pinBState; //NAND pinOutState = !(pinAState & pinBState); //NOR pinOutState = !(pinAState | pinBState); //XNOR pinOutState = !(pinAState ^ pinBState);